Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 9
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
é o círculo
Passo 1
E aiiii turma, beleza?
Nesse exercício devemos usar o teorema de Green para calcular a seguinte integral de linha com orientação positiva:
Onde, é o círculo
Bom, o primeiro passo é esboçar esse gráfico. Repare que temos um círculo de raio igual a Fazendo isso temos:
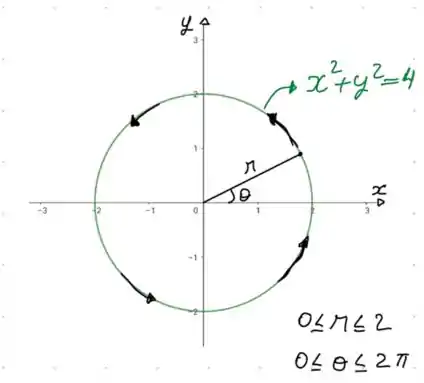
Como temos um círculo, é interessante trabalharmos em coordenadas polares. Logo temos que:
E para esse círculo vamos ter os intervalos de e como:
Vamos lembrar do teorema de Green. Para uma curva fechada e orientada positivamente, ou seja, no sentido anti-horário, podemos aplicar:
Por fim, seu objetivo vai ser montar a integral e calcular seu valor!
Vamos lá!!!
Passo 2
Vamos começar avaliando nossa região.
Sabemos que ela é o círculo:
Quando se trata de um círculo, podemos usar coordenadas polares. Ficando assim:
Pela figura, conseguimos confirmar que é um círculo de raio .
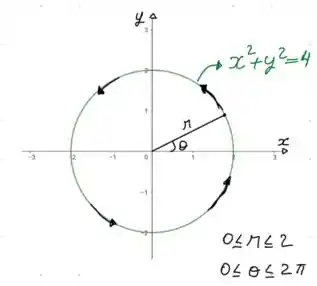
Como é um círculo completo, vamos ter os seguintes intervalos de variação de e :
Passo 3
Como é uma curva fechada, pelo Teorema de Green temos:
Do enunciado temos que nossa integral de linha é:
Onde,
Substituindo no teorema de Green, vamos ter:
Fazendo as derivadas, ficamos com:
Agora devemos substituir por coordenadas polares. Fazendo isso ficamos com:
Vamos utilizar a seguinte relação trigonométrica:
Logo ficamos com:
Passo 4
Agora vamos integrar. Mas antes vamos substitui os limites de integração:
Vamos ficar com:
Integrando em vamos ter:
Aplicando os intervalos de integração, temos:
Integrando em , vamos ter:
Aplicando os intervalos de integração:
Logo, nossa resposta aplicando o teorema de Green é: