Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 12
Use o Use o teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.)
Onde,
consiste no arco da curva de a e o segmento de reta de a .
Passo 1
Faaaaaala meu povo, belezinha!? Vamos nessa!
Usando o Teorema de Green devemos calcular a integral de linha:
Onde,
E consiste no arco da curva de a e o segmento de reta de a .
E antes de começar devemos verificar a orientação da curva .
Tá, mas por onde eu começo?
Vamos fazer um esboço da curva . Repare que temos um círculo trigonométrico, logo fazendo o esboço temos:
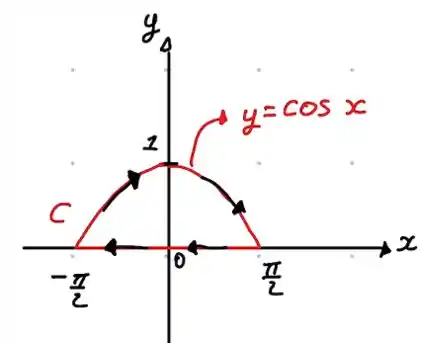
Perceba que ao representar o caminho indicado temos uma curva no sentido horário.
O Teorema de Green é definido para curvas no sentido anti-horário:
Mas calma, podemos usar o teorema de Green se adotarmos o caminho com sentido negativo, como assim? Dessa forma:
Observe também que podemos assumir as seguintes variações dos limites de integração:
Agora não tem erro, é substituir na integral!
Vamos lá colocar mão na massa!
Passo 2
Conseguimos verificar que a curva esta orientada no sentido horário, e para aplicar o teorema de Green devemos fazer a seguinte adaptação:
A partir do campo , podemos identificar o P e Q da seguinte forma:
Comparando:
Temos que:
Agora, aplicando no teorema de Green ficamos com:
Lembrando que nossa região é delimitada por:
Um ponto muito importante. Lembre-se, que sempre começamos integrando pelo termo que possui função nos limites de integração.
Passo 3
Agora vamos aplicar as derivadas. Fazendo isso, ficamos com a seguinte integral:
Substituindo os intervalos de integração, temos:
Integrando em , vamos ter:
Aplicando os limites de integração, teremos:
Agora, vamos ter que fazer a seguinte substituição trigonométrica:
Substituindo, temos:
Vamos separar essa soma em mais integrais, desse jeito:
Vamos precisar fazer uma integral por partes, para a primeira integral, e uma substituição na última integral.
Passo 4
Aplicando integral por partes, em:
Vamos ter:
Vamos chamar:
Substituindo, ficamos com:
Integrando, vamos ter:
Para a última integral:
Temos que aplicar uma substituição, assim:
Substituindo, ficamos com:
Integrando e voltando para a variável , temos:
Passo 5
Substituindo essas respostas na integral e resolvendo a integral do meio:
Vamos ter:
Aplicando os limites de integração. Aqui vai ficar uma conta muito extensa, então vamos simplificar aplicando as seguintes relações que já conhecemos:
Assim, vamos ter:
Assim, concluímos que aplicando o Teorema de Green, obtemos a seguinte resposta: