Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 13
Use o Use o teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.)
Onde, é o circulo orientado no sentido horário.
Passo 1
E aai galerinha, tudo bem!? Bora lá!
A partir do Teorema de Green devemos calcular a integral de linha:
Onde,
Sendo, que é o circulo orientado no sentido horário.
Antes de começar devemos verificar a orientação da curva .
Tá, mas por onde eu começo?
Vamos começar fazendo um esboço da curva . Repare que temos um círculo que está com seu centro em e possui raio igual a . Temos o seguinte desenho:
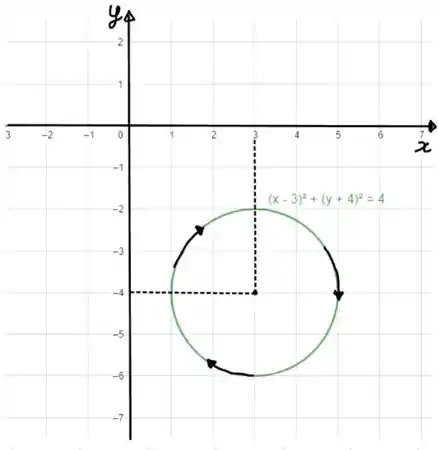
Veja que no caminho indicado temos uma curva no sentido horário, conforme o enunciado menciona.
O Teorema de Green é definido para curvas no sentido anti-horário:
Mas podemos usar o teorema de Green se adotarmos o caminho com sentido negativo, como assim? Dessa forma:
Essa questão, como se trata de um circulo completo, podemos usar coordenadas polares para parametrizar. Desse jeito:
Mas você vai perceber que não vamos precisar fazer isso, ao aplicar o teorema de Green.
Então, vamos começar turma!
Passo 2
Como a curva está orientada no sentido horário, para poder aplicar o teorema de Green devemos fazer a seguinte adaptação:
A partir do campo , podemos identificar o P e Q da seguinte forma:
Comparando:
Temos que:
Agora, aplicando no teorema de Green ficamos com:
Derivando, vamos ter:
Passo 3
Simplificando um pouco, ficamos com:
Por esse motivo que não vamos precisar dos limites de integração! Porque a integral dupla de é igual a área , e conhecemos a área de uma circunferência.
Logo, aplicando o teorema de Green concluímos que:
A área de uma circunferência é:
Como o raio do circulo é igual a . Vamos ter que aplicando o teorema de Green:
Passo 4
Como adendo, podemos provar que o que fizemos no passo anterior está correto.
Tínhamos a integral:
Como é um círculo completo de raio , em coordenadas polares temos:
Substituindo na integral, temos:
Integrando em , temos:
Aplicando os limites de integração, ficamos com:
Integrando em , temos:
Aplicando os limites de integração, vamos ter como resposta:
Viu só, exatamente o que obtemos no passo .