Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 14

Use o Use o teorema de Green para calcular ∫ C F → ⋅ d r → . (Verifique a orientação da curva antes de aplicar o teorema.)

F → x , y = x 2 + 1 i → + tan - 1 ⁡ x j →

Onde, C é o triângulo de ( 0,0 ) a ( 1,1 ) a ( 0,1 ) a ( 0,0 ) .

Passo 1

Faaaala turma, tudo bem?

Devemos usar o Teorema de Green para calcular a integral de linha a seguir:

∫ C F → ⋅ d r →

F → x , y = x 2 + 1 i → + tan - 1 ⁡ x j →

Onde C é o triangulo de segmento de reta de ( 0,0 ) a ( 1,1 ) a ( 0,1 ) a ( 0,0 ) .

Vish, e agora???

Nosso primeiro objetivo é entender a região C . A orientação dada dos vértices do trianguilo, podemos concluir que:

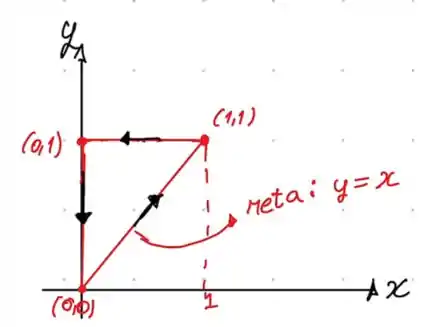
Olhando para a figura, podemos concluir que nossa região é fechada, orientada no sentido anti-horário e os intervalos de variação de x e y são:

0 ≤ x ≤ 1

x ≤ y ≤ 1

Pelo Teorema de Green, podemos relacionar uma integral de linha em uma curva fechada C como uma integral dupla de área. Desse jeito:

∫ C F → ⋅ d r → = ∬ D ∂ Q ∂ x - ∂ P ∂ y d x d y

Onde, P e Q são respectivamente no vetor F :

F x , y = P i + Q j

Com esse bizu, agora já podemos montar nossa integral e resolvê-la.

Vamos nessa!!!

Passo 2

Já verificamos que nossa região está no sentido anti-horário e que os intervalos de integração são:

0 ≤ x ≤ 1

x ≤ y ≤ 1

Observe novamente a imagem formada pelos vértices do triangulo:

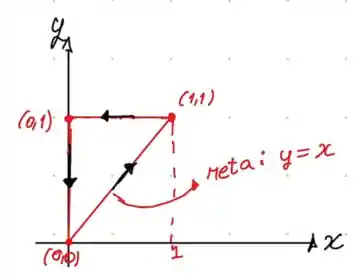
Como ela esta orientada no sentido anti-horário, isso confirma que podemos utilizar o Teorema de Green. Onde:

∫ C F → ⋅ d r → = ∬ D ∂ Q ∂ x - ∂ P ∂ y d x d y

Onde, P e Q são respectivamente no vetor F :

F x , y = P i + Q j

Passo 3

Do enunciado sabemos que nossa força F é:

F → x , y = x 2 + 1 i → + tan - 1 ⁡ x j →

Logo P e Q são:

P = x 2 + 1

Q = tan - 1 ⁡ x

Agora vamos substituir no Teorema de Green. Ficando com:

∬ D ∂ ∂ x ( tan - 1 ⁡ x ) - ∂ ∂ y ( x 2 + 1 ) d x d y

Derivando e substituindo os intervalos de integração que são:

0 ≤ x ≤ 1

x ≤ y ≤ 1

Temos:

∫ 0 1 ∫ x 1 1 1 + x 2 d y d x

Vale lembrar, que sempre que um intervalo de integração depender de funções, ele deve ser integrado primeiro.

Agora, devemos integrar primeiro em d y .

Passo 4

Integrando em d y , vamos ter:

∫ 0 1 1 1 + x 2 y x 1 d x

Aplicando os limites de integração ficamos com:

∫ 0 1 1 - x 1 + x 2 d x

Agora, devemos integrar em d x . Mas antes vamos separar em duas integrais:

∫ 0 1 1 1 + x 2 d x - ∫ 0 1 x 1 + x 2 d x

A primeira integral é bem conhecida, sua resposta é:

∫ 1 1 + x 2 d x = tan - 1 ⁡ x

Na segunda devemos fazer uma substituição do tipo:

u = 1 + x 2

d u 2 = x   d x

Substituindo na integral, temos:

∫ 0 1 1 1 + x 2 d x - ∫ 0 1 1 u d u 2  

Passo 5

Resolvendo as integrais, e voltando para a variável x temos:

tan - 1 ⁡ x - 1 2 ln ⁡ 1 + x 2 0 1

Aplicando os intervalos de integração ficamos com:

tan - 1 ⁡ 1 - 1 2 ln ⁡ 1 + 1 2 - tan - 1 ⁡ 0 - 1 2 ln ⁡ 1 + 0 2

Vamos olhar um gráfico da tan - 1 ⁡ x :

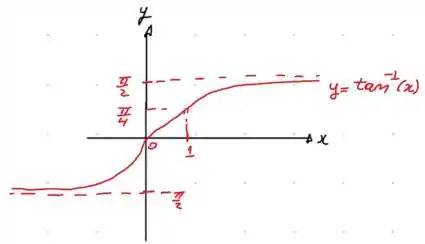
Assim, concluímos que:

tan - 1 ⁡ 1 = π 4

tan - 1 ⁡ 0 = 0

Também sabemos que:

ln ⁡ 1 = 0

Logo, temos que nossa resposta é:

π 4 - 1 2 ln ⁡ 2 - 0 - 0

π 4 - 1 2 ln ⁡ 2

Resposta

∫ C F → ⋅ d r → = π 4 - 1 2 ln ⁡ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = ( x + 3 y ) i + ( 2 x - y ) j
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = t g - 1 ⁡ y x i + l n ⁡ x 2 + y 2 j C : A frontei
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circula-ção em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = ( x - y ) i + ( y - x ) j C : O quadrado limitad
O que é o teorema de Green? Como se pode interpretá-lo?
Utilize o teorema de Green para encontrar a circulação anti-horária e o fluxo exterior para os campos e curvas nos Exercícios 49 e 50.Triângulo F = y - 6 x 2 i + x + y 2 j . C: O triângulo formado pel