Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 3b
Mude de coordenadas retangulares para cilíndricas.
(b)
Passo 1
Faala, pessoal!
Nessa questão a gente precisa mudar esse ponto de coordenadas retangulares para coordenadas cilíndricas .
Pra isso, a gente tem que usar da relação entre essas coordenadas.
A coordenada não muda! Já e se relacionam com e da mesma forma que fazíamos em coordenadas polares. Então:
Com isso, nós temos essas relações pra mudar de para :
O que vamos fazer é aplicar essas relações pra achar e .
Passo 2
Em coordenadas retangulares, nosso ponto é , então:
Para achar :
Então:
Lembra que representa um raio, então sempre vai ser positivo!
Para :
Entre e , temos dois valores de que têm tangente igual a , como podemos ver no círculo trigonométrico:
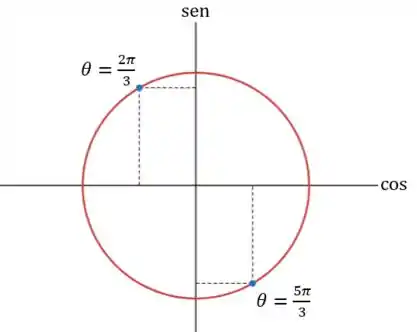
Só que dos valores de e a gente consegue saber o sinal do seno e cosseno:
Das nossas duas opções, a que tem seno positivo e cosseno negativo é
Então já temos nosso ponto: