Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 15
Esboce o sólido cujo volume é dado pela integral e calcule-a.
Passo 1
E aii, pessoal, tudo bem?
Nessa questão, precisamos esboçar o sólido que essa integral representa, depois calcular!
Percebe que como o integrando é , e estamos em coordenadas cilíndricas, isso é o equivalente a:
Já que esse representa o jacobiano da transformação de coordenadas cartesianas pra cilíndricas.
Então o sólido que queremos é o próprio , que é o domínio dessa integral.
Pra esboçarmos , vamos olhar para os limites de integração de cada uma das variáveis, que nos dá:
A gente vai olhar primeiro pra coordenada , depois as coordenadas e vão ser usadas pra gente ver a projeção do sólido no plano (que é o equivalente a coordenadas polares).
E ai conseguimos esboçar.
Por último, vamos calcular essa integral iterada, de dentro pra fora.
Passo 2
Vamos olhar para os limites das coordenadas cilíndricas, começando pelo :
Nosso sólido está limitado por baixo pelo plano (), então estamos na parte positiva de . Além disso, ele está limitado por cima pela superfície:
Isso é um paraboloide! Se não lembrar disso de cara, podemos transformar em coordenadas cartesianas – já que :
Que é a equação cartesiana de um paraboloide.
Então já sabemos que nosso sólido está entre o plano (roxo) e um paraboloide (verde):
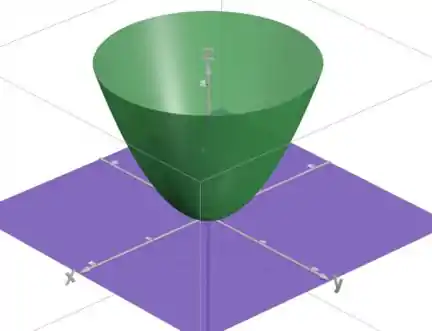
Agora vamos usar as outras duas coordenadas para ver a projeção do sólido:
O entre e quer dizer que a projeção está dentro de uma circunferência de raio .
Já o entre e quer dizer que estamos na parte positiva de :
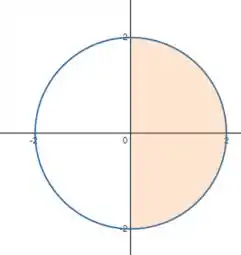
Vamos colocar tudo isso no e esboçar o sólido:
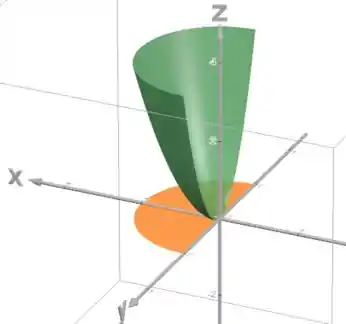
Então o sólido fica assim:
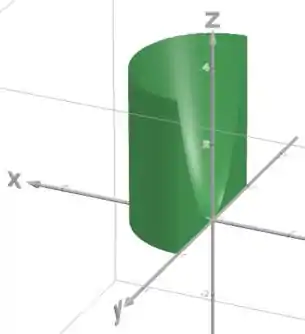
Passo 3
Agora vamos calcular a integral iterada, de dentro pra fora.
Primeiro, em função de , considerando e constante:
Substituindo os limites:
Agora integramos em função de , com constante:
Então:
Podemos tirar a constante da integral e simplificar:
Por último, integramos em função de :
Então:
Resposta
