Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 39
Use o Teorema de Pappus e o fato de que o volume de uma esfera de raio é para mostrar que o centroide da lâmina limitada pelo eixo e o semicírculo é (Esse problema foi resolvido diretamente no Exemplo 3.)
Passo 1
O Teorema de Pappus diz que, para um sólido de revolução gerado pela rotação de uma região :
Vamos imaginar que o nosso sólido seja a esfera, obtida pela rotação do semicírculo em torno do eixo .
Queremos a partir dessas informações, chegar no centroide dessa lâmina. Vem comigo!
Passo 2
Essa é a nossa lâmina:
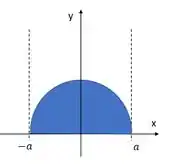
Vemos que pela simetria:
Passo 3
Vamos usar o teorema para achar a coordenada . Ele diz que:
Já temos o volume da esfera:
A área de é a área de um semicírculo:
A distância percorrida pelo centroide, na rotação para a obtenção do sólido, é o comprimento de uma circunferência de raio , já que a rotação é em torno do eixo . Então podemos escrever:
Substituindo tudo que a gente tem na fórmula do teorema:
Isolando :
Provamos então que o centroide está em:
O que foi pedido. Uhul!
Resposta
Prova nos passos