Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 38
Prove que o centroide de um paralelogramo é o ponto de interseção das diagonais do paralelogramo. [Sugestão: Escolha as coordenadas de tal modo que os vértices do paralelogramo estejam localizados em e ]
Passo 1
A gente precisa provar que o centroide de um paralelogramo está na interseção das diagonais. O enunciado manda a gente partir de um paralelogramo assim:
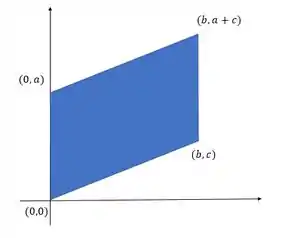
Podemos tentar usar as integrais para provar isso, mas há um jeito mais direto. Pensando na definição do centroide. Vem comigo!
Passo 2
Podemos definir o centroide de uma lâmina, se ela tiver densidade constante por toda sua área, como o ponto onde há equilíbrio de momentos.
Agora pensa comigo. Vamos desenhar uma das diagonais do centroide:
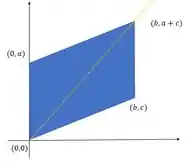
Percebe que ele divide o paralelogramo em áreas iguais? Como a densidade é constante, isso diz para gente que ao longo dessa diagonal há equilíbrio de momentos.
Ao longo da outra diagonal também haverá equilíbrio de momentos, as áreas também são iguais.
Se fizermos a interseção entre duas linhas de equilíbrio, encontramos o ponto de equilíbrio, o centroide!
Agora um bizu: sempre que tivermos duas retas diferentes e não coincidentes que dividem uma região em duas áreas iguais, a interseção delas é o centroide.
Provamos usando nossos conceitos. Uhul!
Resposta
Prova nos passos