Use o Teorema de Pappus e o resultado do Exercício 39 para calcular o volume do sólido gerado quando a região limitada pelo eixo e o semicírculo gira em torno da

(a) reta

Temos o semicírculo que vai ser girado em torno dessa reta em verde. Para calcular o volume do sólido que vai surgir, pelo Teorema, precisamos entender como calcular a distância percorrida pelo centroide nessa rotação.

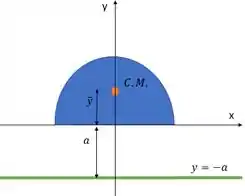
Agora pensa comigo: a trajetória do centroide é uma circunferência. E o raio dela é igual à distância do centroide até o eixo de rotação, no nosso caso a reta .

Então, podemos dizer que nossa trajetória vai ter um raio de:

E a distância percorrida pelo centroide é o comprimento da trajetória, que é uma circunferência. Logo, é só a gente calcular o comprimento da circunferência:

Precisamos da área da região. A área de é a área de um semicírculo, então:

Com tudo calculado, podemos usar:

Substituindo tudo que a gente tem na fórmula do teorema:

Mas lembra que a gente sabe que:

Aí nossa continha fica:

Arrasamos!