Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.5 - Ex. 72
Use o teorema do valor intermediário nos Exercícios 71 -78 para provar que cada equação tem uma solução. Em seguida, utilize uma calculadora gráfica ou um computador com software gráfico para resolver as equações.
72.
Passo 1
Bora lá então. Vamos achar primeiro o
Agora o
Opa, já achamos um intervalo que mostra uma raiz, já que mudou o sinal. Bora dar continuidade.
.
O sinal mudou mais uma vez...temos mais uma raiz entra 0 e 1.
Pra concluir, f(2)
Pronto, com isso a gente consegue os três intervalos em que as raízes se encontram.
Passo 2
Agora vem comigo e da uma olhada no esboça pra ver se a gente está certo!
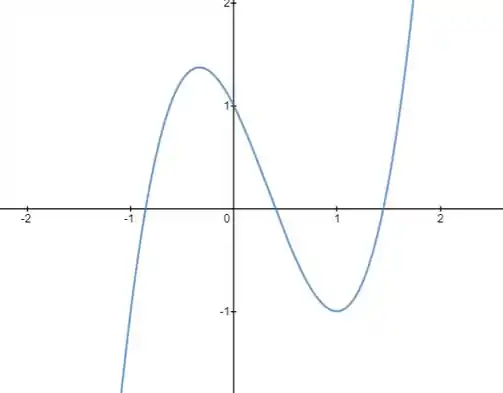
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o teorema do valor intermediário nos Exercícios 71 -78 para provar que cada equação tem uma solução. Em seguida, utilize uma calculadora gráfica ou um computador com software gráfico para resolver
Use o teorema do valor intermediário nos Exercícios 71 -78 para provar que cada equação tem uma solução. Em seguida, utilize uma calculadora gráfica ou um computador com software gráfico para resolver
Use o teorema do valor intermediário nos Exercícios 71 -78 para provar que cada equação tem uma solução. Em seguida, utilize uma calculadora gráfica ou um computador com software gráfico para resolver
Use o teorema do valor intermediário nos Exercícios 71 -78 para provar que cada equação tem uma solução. Em seguida, utilize uma calculadora gráfica ou um computador com software gráfico para resolver