Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 1
Para a função cujo gráfico é dado, determine os seguintes limites.
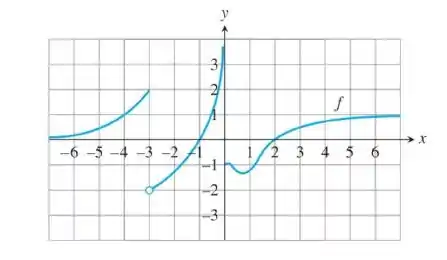
Passo 1
Essa daqui a gente faz na base do olhômetro mesmo, até por que a gente não tem a função escrita.
Passo 2
Só olhando ali o valor da função quando o x está em 2. Tenho certeza que você concorda comigo então que esse limite vale 0, certo?
Passo 3
Agora vai ser exatamente o mesmo procedimento pra todos os outros pontos.
- Como para existem limites diferentes, no 3 mesmo então não vai existir limite.
- mesma justificativa da letra d.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
43. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = 2 x 2 + x - 1 x 2 + x - 2
42. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = x 2 + 1 2 x 2 - 3 x - 2
46. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = 2 e x e x - 5
51. Uma função f é a razão de duas funções quadráticas e possui uma assíntota vertical x = 4 e somente um intercepto com o eixo das abscissas em x = 1 . Sabe-se que f possui uma descontinuidade removí
Encontre os limites quandox → ∞ e quando x → - ∞ Use essa informação, bem como as intersecções com os eixos, para fazer um esboço do gráfico, como no Exemplo 12. y = x 4 - x 6