Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.3 - Ex. 7
Use o teste da integral para determinar se as séries nos Exercícios 1-10 convergem ou divergem. Certifique-se de que as condições do teste da integral sejam satisfeitas.
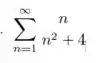
Passo 1
Fala galerinha, tranquilidade, esse problema se baseia no teste da integral, para fazer esse teste precisamos comparar a série com uma função que obedece algumas condições. Precisa ser decrescente, positiva e contínua, para , com isso saberemos que tanto a série quanto a integral convergem
Um extra é que elas não precisam ter o mesmo valor para serem convergentes.
Passo 2
Identificar a função comparável, que seja contínua, positiva e decrescente:
Nesse caso temos que verificar se é decrescente com isso vamos fazer a primeira derivada:
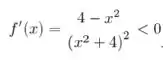
Esse resultado para x>2, porém ela é decrescente a partir de x maior igual a 3
Passo 3
Agora resolvermos a integral para da seguinte forma:
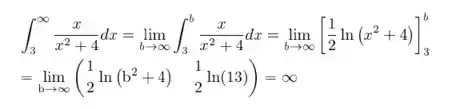
Resposta
Como a integral é divergente então a série do problema também é divergente