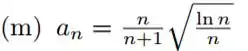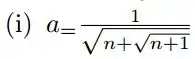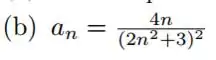Exercícios de Teste da Comparação no Limite - Lista de Exercícios Resolvida

Determine para quais valores de a série:

É convergente e para quais é divergente.

Determine se a série converge ou diverge

Determine se a série converge ou diverge

Decida se a série converge condicionalmente ou absolutamente ou diverge

Determine se a série converge ou diverge

4 – Decida se a afirmação dada é (sempre) verdadeira ou (às vezes) falsa. Justifique sua resposta dando um argumento lógico matemático ou um contra-exemplo.

a) se converge, então converge absolutamente.

Determine se a série converge ou diverge

4 – Decida se a afirmação dada é (sempre) verdadeira ou (às vezes) falsa. Justifique sua resposta dando um argumento lógico matemático ou um contra-exemplo.

b) A sequência converge.

1 – Teste a convergência ou divergência das séries, mencione o teste utilizado.

b)

1 – Teste a convergência ou divergência das séries, mencione o teste utilizado.

d)

Determine quais dentre as séries abaixo convergem e quais divergem:

Determine se a série converge ou diverge

Verifique a convergência ou divergência da sequencia e das séries numéricas abaixo:

(3.2)

Quais das séries abaixo são condicionalmente convergentes e quais são absolutamente convergentes (justifique sua resposta):

Encontre os valores de para os quais a série

É convergente.

Questão 3) Determine, em cada item, se a série é convergente ou divergente, determinando também qual é o modo de convergência. Especifique os testes utilizados.

c)

Questão 2: Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente:

Estude a convergência, convergência absoluta ou divergência da série abaixo:

Em relação à série , tem-se que:

2. A série:

Em relação à série , tem-se que:

2. A série:

Em relação à série , tem-se que:

2. A série:

Em relação à série , tem-se que:

2. A série:

Em relação à série , tem-se que:

2. A série:

Classificar em convergente ou divergente a série numérica

Decida se a série converge condicionalmente ou absolutamente ou diverge

Seja um número real fixado. Determine todos os valores de para os quais a série

Converge.

Determine se a série

é convergente ou divergente explicitando o teste utilizado.

Determine se a série converge ou se diverge.

Seja uma sequência tal que

Em relação à série

é correto afirmar:

Se a série converge, então

Se a série converge, então

A série converge.

A série converge se, e somente se, .

Em relação à sequência é correto dizer:

Escolha uma ou mais:

1. É crescente
2. É limitada inferiormente por e , logo diverge.
3. É limitada superiormente por , logo converge.
4. Converge a zero.
5. É limitada superiormente por , logo diverge

Diga se as sequências são convergentes ou divergentes. Se convergir, encontre o limite

Diga se as sequências são convergentes ou divergentes. Se convergir, encontre o limite

Diga se as sequências são convergentes ou divergentes. Se convergir, encontre o limite

Verifique se as séries convergem ou divergem.

(Capítulo 11.5 – Exercício 32) Para quais valores de a serie e convergente?

Determine para quais valores de a série:

É convergente e para quais é divergente.

(Capítulo 11.4 – Exercício 17) Determine se a série converge ou diverge.

(Capítulo 11.5 – Exercício 5) Teste a série quanto a convergência ou divergência.

(Capítulo 11.5 – Exercício 6) Teste a série quanto a convergência ou divergência.

(Capítulo 11.5 – Exercício 7) Teste a série quanto a convergência ou divergência.

(Capítulo 11.5 – Exercício 8) Teste a série quanto a convergência ou divergência.

(Capítulo 11.4 – Exercício 46) Se e forem ambas séries convergentes com termos positivos, é verdade que também será convergente?

Determine se a série converge ou diverge

Determinar se a série abaixo é absolutamente convergente, condicionalmente convergente ou divergente:

Das seguintes séries marque quantas divergem.

Escolha uma opção:

3 – Quais das seguintes séries numéricas convergem e quais divergem? Justifique sua resposta.

b) .

Considere a série , selecione a resposta correta

1. A série é divergente por comparação com
2. A série é convergente por comparação com
3. A série é convergente por comparação com
4. A série é divergente por comparação com

Considere a série , selecione as respostas corretas

Escolhe uma ou mais

1. Tomando , temos logo nada podemos concluir
2. A igualdade é verdadeira
3. Usando os dois itens anteriores, podemos mostrar que é convergente

Em relação à série , tem-se que:

2. A série:

Determine se a série converge absolutamente, se converge condicionalmente ou se diverge.

4 – Decida se a afirmação dada é (sempre) verdadeira ou (às vezes) falsa. Justifique sua resposta dando um argumento lógico matemático ou um contra-exemplo.

b) A sequência converge.

4 – Decida se a afirmação dada é (sempre) verdadeira ou (às vezes) falsa. Justifique sua resposta dando um argumento lógico matemático ou um contra-exemplo.

a) se converge, então converge absolutamente.

Determine se cada série a seguir converge absolutamente, condicionalmente ou diverge:

Considere a série , sendo que:

Determine se a série converge ou diverge.

Questão 1: Estude a convergência, convergência absoluta ou divergência das séries abaixo.

1. Determine se a sentença abaixo é verdadeira ou falsa:

Se é uma série convergente de termos positivos, então converge.

Quais das sequências convergem e quais divergem ? Ache o limite de cada seqüência convergente :

a )

Quais das sequências convergem e quais divergem ? Ache o limite de cada seqüência convergente :

b )

Quais das sequências convergem e quais divergem ? Ache o limite de cada seqüência convergente :

c )

Quais das sequências convergem e quais divergem ? Ache o limite de cada seqüência convergente :

e )

Quais das sequências convergem e quais divergem ? Ache o limite de cada seqüência convergente :

d )

Quais das sequências convergem e quais divergem ? Ache o limite de cada seqüência convergente :

f )

Quais das sequências convergem e quais divergem? Ache o limite de cada sequência convergente :

g)

Quais das sequências convergem e quais divergem? Ache o limite de cada sequência convergente :

h)

Quais das sequências convergem e quais divergem? Ache o limite de cada sequência convergente :

i)

8 - Determine se a série converge ou diverge.

x)

9 - Determine se a série converge ou diverge.

a)

9 - Determine se a série converge ou diverge.

b)

9 - Determine se a série converge ou diverge.

h)

(Miscelânea) Quais das séries abaixo convergem e quais divergem? Justifique suas respostas. (Observação: em alguns casos pode existir mais de uma maneira de determinar a convergência ou divergência da série.)

g)

(Miscelânea) Quais das séries abaixo convergem e quais divergem? Justifique suas respostas. (Observação: em alguns casos pode existir mais de uma maneira de determinar a convergência ou divergência da série.)

o)

Exercício 20. Verifique quais das séries abaixo são convergentes (sem necessariamente calcular o limite).

a) ;

Exercício 20. Verifique quais das séries abaixo são convergentes (sem necessariamente calcular o limite).

h) ;

Use o Teste da Comparação para achar quais das séries convergem e quais divergem:

a)

Use o Teste da Comparação para achar quais das séries convergem e quais divergem:

b)

Use o Teste da Comparação para achar quais das séries convergem e quais divergem:

c)

Use o Teste da Comparação no Limite para achar quais das séries convergem e quais divergem:

a)

Use o Teste da Comparação no Limite para achar quais das séries convergem e quais divergem:

c)

Use o Teste da Comparação no Limite para achar quais das séries convergem e quais divergem:

b)