Use triângulos de referência como no exemplo 1 para determinar os ângulos nos exercícios abaixo:
a)
Passo 1
Bom, primeiro precisamos saber qual o ângulo estamos trabalhando. Ok?
Para isso, vamos utilizar a seguinte tabela para os ângulos geralmente usados na trigonometria, beleza?

Quando queremos a queremos saber qual o arco cuja tangente é ou seja
De acordo com a tabela acima sabemos que esse ângulo é o ou 60 º. Beleza?
Então agora vamos ao triângulo solicitado na questão:
Passo 2
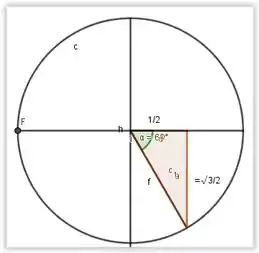
Resposta
Escrever só a resposta aqui quando o problema tiver resposta