Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.2 - Ex. 36
36. Uma escada com 7m de comprimento está apoiada em uma parede vertical. Se a base da escada for puxada horizontalmente de tal forma que se afaste da parede e que o topo escorregue a uma velocidade de 1m/s , qual a velocidade com que a medida do ângulo entre a escada e o chão estará variando quando o pé da escada estiver a 4m da parede?
Passo 1
Este problema, é um problema clássico de taxas relacionadas. Para resolver problemas deste tipo, basta esboçar o que foi dito no enunciado, encontrar a função que relaciona as variáveis disponíveis no esboço e derivar a função de interesse. Neste caso, devemos encontrar a taxa de variação do ângulo entre a escada e o chão em função do tempo.
Passo 2
Assim, um esboço do que foi dito no enunciado é dado pela seguinte figura:
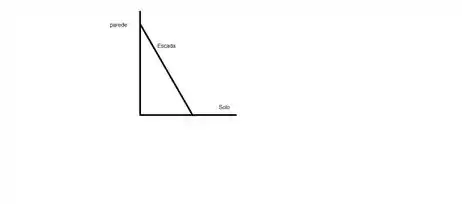
Seja a altura da escada, distância do pé da escada até a parede e o ângulo entre a escada e o chão, podemos escrever a seguinte expressão:
Passo 3
Derivando a expressão acima com relação ao tempo:
Passo 4
Quando , . Então, temos que . Substituindo, , e na equação acima: