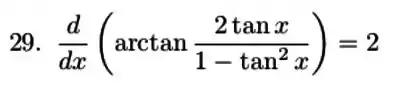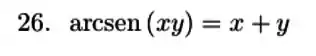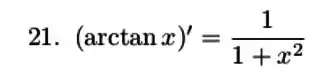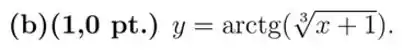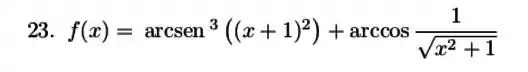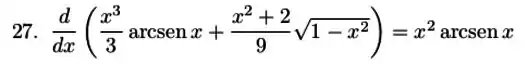Exercícios de Derivadas de Funções Inversas Trigonométricas - Lista de Exercícios Resolvida
Questão 2
Calcule o que se pede:
Seja , onde a função é diferenciável. Calcule se conhecemos a informações: ; ; .
Ver solução completaQuestão 4
Calcule a derivada de .
Use a informação da questão anterior para mostrar que
Ver solução completaQuestão 16
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
c.
Ver solução completaQuestão 24
4. Uma função está definida implicitamente pela equação
Determine e e a equação da reta tangente ao gráfico de no ponto .
Ver solução completaQuestão 26
6. Para quais valores de o gráfico de tem uma reta tangente horizontal? Se não tem, por que não?
f.
Ver solução completaQuestão 29
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
d.
Ver solução completaQuestão 30
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
e.
Ver solução completaQuestão 31
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
Questão 37
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 38
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 39
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 41
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 42
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 43
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 44
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 48
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
d.
Ver solução completaQuestão 49
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
e.
Ver solução completaQuestão 50
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
c.
Ver solução completaQuestão 51
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
Questão 52
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
b.
Ver solução completaQuestão 53
2) Seja
Considere
- Mostre que a função é inversível em todo o seu domínio
- Determine a equação da reta tangente ao gráfico de (a inversa de ) em . Dica: não é necessário determinar
- Determine o domínio de e uma expressão para
Questão 61
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completaQuestão 62
- Uma nova regra de derivação foi deduzida nesse tópico: a derivada da função inversa. A tabela da esquerda representa três formas de escrever a mesma regra, apenas em notações diferentes. A tabela da direita apresenta a derivada das inversas das funções seno, cosseno e tangente (já com a regra da cadeia embutida).

Utilize a tabela para determinar a derivada das funções abaixo.
b.
Ver solução completaQuestão 63
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
Ver solução completa