33. Um letreiro com de altura está colocado em uma parede, sendo que sua base está 2m acima do nível dos olhos de uma mulher que tenta lê-lo. A que distância da parede ela deve ficar para ter uma melhor visão do letreiro, isto é, para o ângulo sob o qual ela vê o letreiro seja máximo?

Um esboço do que está sendo dito no enunciado pode ser representado pela seguinte figura:

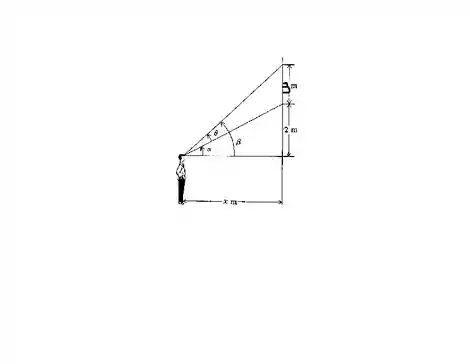
Seja a distância do observador até a parede. Queremos encontrar o valor de que irá tornar um máximo absoluto. Como está no intervalor , o valor máximo absoluto de será um valor máximo relativo. Podemos ver da figura que , vemos também que:

Substituindo esses valores de na relação obtemos :

Derivando com relação a x a função que descreve o comportamento do ângulo em função da distância, teremos:

Igualando a zero o resultado da derivada para encontrar os pontos críticos, vem:

A solução foi rejeitada por não está no intervalor . Como o valor máximo da relativo de é um valor máximo absoluto, concluímos que o observador deve ficar a aproximadamente 3,16 m da parede.