Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.3 - Ex. 30
Utilize uma calculadora gráfica ou um computador para traçar na mesma tela a curva e sua função curvatura . Esse é o gráfico que você esperava?
Passo 1
E aí, galera. Beleza?
A questão quer que a gente faça um gráfico da função dada e de sua função curvatura.
Então, para fazer isso vamos precisar obter a função curvatura, que é dada pela equação:
Assim, o primeiro passo é encontrarmos as primeiras derivadas da função , para depois utilizarmos a equação acima.
Uma vez obtida a função , vamos plotar os dois gráficos.
Vamos lá...
Passo 2
A derivada primeira é dada por:
E a derivada segunda:
Assim,
Aplicando :
Passo 3
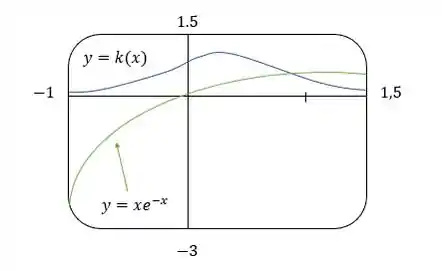
O gráfico de a curvatura aqui é o que esperaríamos.
O gráfico de está dobrando um pouco mais acentuadamente a direita da origem.
Como , o gráfico de é assintótico ao e então a curvatura se aproxima de zero.
Resposta
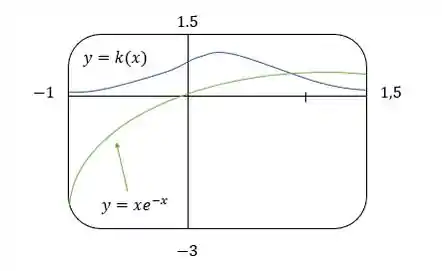
O gráfico de a curvatura aqui é o que esperaríamos. Como , o gráfico de é assintótico ao e então a curvatura se aproxima de zero.