Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 30
A superficie com as equações parametricas
Onde e , é chamada Tira de Mobius. Trace o gráfico dessa superficie com vários pontos de vista. O que há de estranho nela?
Passo 1
Olá, tudo bem? Vamos ver o que a questão quer.
Primeiro, ela dá uma superfície com essas equações paramétricas:
Onde
Segundo, ela diz que essa superfície é chamada Tira de Mobius.
Terceiro e último, ela pede para traçar o gráfico dessa superficie com vários pontos de vista e dizer o que há de estranho nela.
Muito bem!
Essa questão requer que usemos uma calculadora gráfica para montar essa superfície. Você pode verificar isso com o desenho de um gráfico ao lado do número da questão.
Você pode usar qualquer software para fazer esse gráfico!
Então, vamos representar graficamente a superfície como vista de frente, depois a partir de dois pontos de vista adicionais.
E a partir daí, veremos o que está estranho.
Partiu?
Passo 2
Vamos traçar as vistas.
De frente:
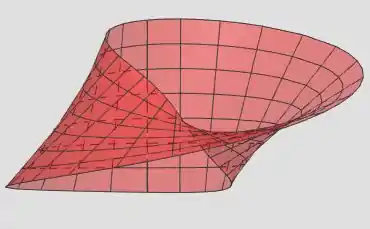
De um ponto adicional:
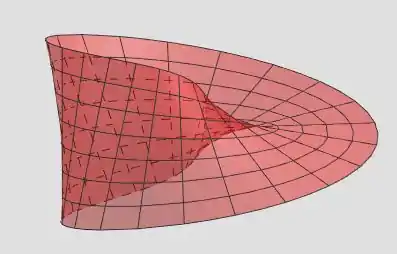
Outro ponto adicional:
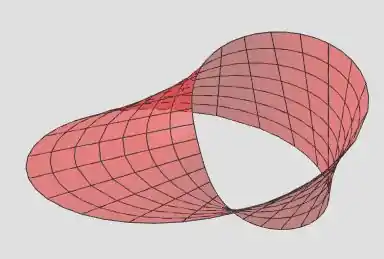
Passo 3
Vamos ver o que está estranho nessas figuras.
O que há de estranho na fita de Mobius é se marcarmos um ponto no interior da fita é possível percorrer ela toda (as duas faces). Se fosse um círculo isso nunca seria possível.
Resposta
O que há de estranho na fita de Mobius é se marcarmos um ponto no interior da fita é possível percorrer as duas faces.