Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 5
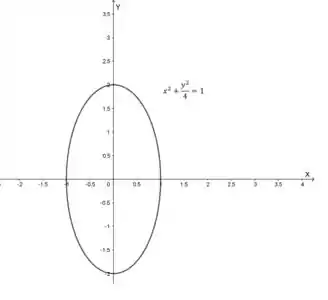
(a) Esboce o gráfico da curva plana com equação vetorial dada.
(b) Determine r’(t).
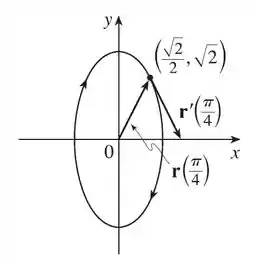
(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.
Passo 1
Então meu amigo. Vamos fazer algumas coisas aqui, a gente tem a curva vetorial:
Precisamos esboçar o gráfico dessa curva. Iremos fazer isso utilizando um software gráfico, mas antes disso, iremos colocar em coordenadas cartesianas. Para isso, a gente pode utilizar de uma identidade trigonométrica e das relações entre coordenadas parametrizadas e cartesianas.
Para derivarmos precisamos derivar cada termo individualmente.
Passo 2
-
As equações paramétricas correspondentes à função vetorial dada são
Sabemos que . Logo, temos:
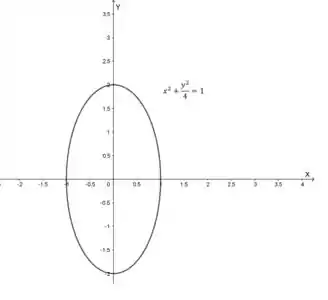
Essa equação é uma outra forma de apresentação da função vetorial . Essa forma é bem mais conhecida por nós e representa uma elipse de parâmetros e . Portanto, o gráfico da curva referente à é
Passo 2
-
Determinamos derivando as componentes de .
Passo 3
O vetor posição em é
Por outro lado, o vetor tangente em , tem origem no ponto (,) e é dado por
Com base nos resultados obtidos podemos representar esses vetores conforme mostrado na figura abaixo:
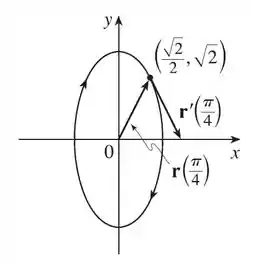
Resposta
