Repita o exercício 15 para a integral
Passo 1
Para calcular as estimativas usando uma calculadora programável, vamos usar o Maple, podemos definir a função (chamando-a de ), carregue o pacote do aluno e use o comando soma intermediária (soma intermediária , ;
Passo 2
para obter a estimativa com quadrados de tamanho igual. A matemática não tem soma especial de Riemann , mas podemos definir e, em seguida, usar comandos aninhados para calcular as estimativas.
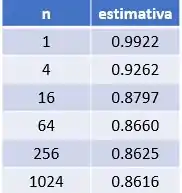
Resposta
Ei, a resposta está no passo a passo :)