Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.3 - Ex. 8

Utilize o computador para traçar o gráfico da curva com equações paramétricas , , . Determine o comprimento total da curva com precisão de quatro casas decimais.

Passo 1

Olá, meu querido estudante. Vou resolver essa atividade com você.

Temos a curva parametrizada dada por:

E precisamos utilizar um software para traçar o gráfico dessa curva. Aqui a gente irá utilizar o Desmos, por ser online.

Já para encontrarmos o comprimento total da curva, deveremos utilizar então a fórmula:

Passo 2

Então para criarmos a figura iremos fazer o seguinte, no site do desmos 3D iremos inserir:

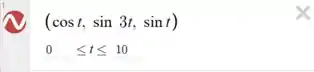
E com isso iremos gerar a figura:

Assim, vamos calcular, primeiro, as derivadas:

Assim

Utilizando a identidade trigonométrica fundamental para simplificar, e uma calculadora cientifica para resolver e essa integral:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Determine os vetores tangente e normal unitários T(t) e N(t).(b) Utilize a Fórmula 9 para encontrar a curvatura. r t = 1 3 t 3 ,t 2 ,2 t

Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t = t i + t j + c o s c o st k

Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t = t 2 i + t 4 j + t 6 k

Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q . P 0,0 , 0 Q ( 1,2 , 3 )

Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t =t , cos ⁡ 2 t , sin ⁡ 2 t