Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 9
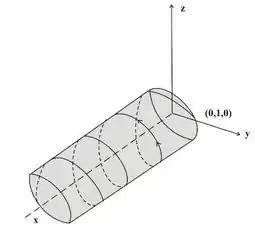
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.
Passo 1
Eaee, belezinha?? Bom... Queremos esboçar o gráfico da seguinte função paramétrica, mostrando a direção em que o parâmetro cresce:
Para isso, precisamos primeiro definir quem são , e com relação ao parâmetro .
Em seguida, deveremos procurar uma relação que envolva pelo menos duas dessas variáveis para que torne mais simples a nossa plotagem.
Sei que é uma sugestão bem ampla, mas já já você vai entender!! 😉
Por fim, iremos indicar com setas a direção na qual o parâmetro cresce.
Para isso, basta aplicarmos alguns valores de em uma determinada ordem (preferencialmente crescente) e analisar como a curva se comporta!!
Agora bora lá!! 😉
Passo 2
Se , então:
Agora vamos procurar alguma relação que envolva essas variáveis.
Lembra que ??
Isso quer dizer que e se comportam como uma circunferência. E, como , no plano tridimensional a gente vai ter um cilindro!!!
Quer entender melhor? Se liga aqui embaixo:
Vamos calcular para entender melhor o gráfico:
Então a curva paramétrica está “presa” no cilindro .
Passo 3
Levamos em consideração o valor:
Vemos que a curva gira em relação ao eixo linearmente ao redor do cilindro. É uma hélice!!
Assim, aqui a gente nem vai precisar analisar os valores de , sabe por quê?
Porque olhe só... na medida que aumentamos , aumenta na mesma proporção!!!
Dessa forma, temos a nossa figura:
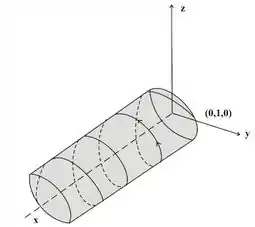
Resposta
