Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 3
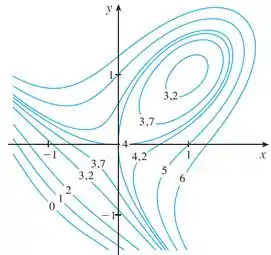
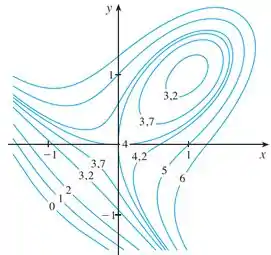
Utilize as curvas de nível da figura para predizer a localização dos pontos críticos de e se tem um ponto de sela ou um máximo ou mínimo local em cada um desses pontos. Explique seu raciocínio. Em seguida, empregue o Teste da Segunda Derivada para confirmar suas predições.
Passo 1
Show de bola, galera.... Questãozinha com curvas de nível, vamos lá!
A questão nos as curvas de nível da função
E nos pede para predizer os pontos críticos de !
Pra procurar esses pontos a gente deve observar o comportamento das curvas de nível: Quando temos várias curvas em elipse, uma “dentro” da outra em sequência, nós já podemos associar com um máximo ou mínimo!
Da mesma forma, quando temos curvas que “desenham um x” ou parecem se afastar de um ponto, podemos associar estas com um ponto de sela!
Em seguida nós vamos usar a seguinte fórmula para confirmar se a gente acertou os pontos
Onde se
então é um mínimo local.
então é um máximo local.
então não é nem mínimo e nem máximo local.
Passo 2
Ao observarmos aquelas curvas de nível ali em cima, percebemos que o ponto é um forte candidato a mínimo local, uma vez que parece haver um vale ao redor delem já que a função cresce em valor quando nos afastamos desse ponto por todas as direções.
Já o ponto é um possível candidato a ponto de sela, uma vez que a função cresce em valor quando nos afastamos desse ponto por uma direção, mas decresce quando nos afastamos por outra.
Passo 3
Já temos os possíveis pontos e , agora vamos montar a expressão do Teste da Derivada Segunda para aplicá-los!
Seja
Precisamos então de , e , de forma que:
Para , precisamos encontrar em derivar novamente em
E da mesma forma, para nós derivamos a função em
E para
De forma que temos
Dessa forma, para o ponto temos
De forma que o nosso ponto é um ponto de sela, assim como previmos!
E para o ponto
E
De forma que o nosso ponto é um ponto de mínimo!
Resposta
é um ponto de sela e é um ponto de mínimo.