Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.7 - Ex. 17

14.17. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no computador, utilize-o com a janela de inspeção e o ponto de vista que mostre os aspectos importantes da função.

f x , y = x 2 + y 2 e y 2 - x 2

Passo 1

A gente tem que determinar os pontos extremos da nossa função, e depois ver se são pontos de mínimo, de máximo ou um ponto de sela.

Para a gente fazer isso, a gente tem que trabalhar com as derivadas, acontece o seguinte, a gente deriva a função e iguala a derivada à 0, então nós teremos nosso ponto de interesse.

Vamos começar determinando nossas derivadas

f x , y = x 2 + y 2 e y 2 - x 2

Vamos derivar primeiro em relação à x , vamos usar a regra do produto para derivar. A regra do produto é a seguinte:

f x = h ' ⋅ g + h ⋅ g '

Vamos fazer

h = ( x 2 + y 2 )

Então

h ' = 2 x

E

g = e y 2 - x 2

Então

g ' = - 2 x e y 2 - x 2

Agora a gente pode fazer a derivada

f x = 2 x e y 2 - x 2 + x 2 + y 2 - 2 x e y 2 - x 2

Simplificando

f x = 2 x e y 2 - x 2 ( 1 - x 2 - y 2 )

Agora a gente faz a derivada em relação a y , e vamos usar a mesma estratégia, regra do produto

f y = h ' ⋅ g + h ⋅ g '

Vamos fazer

h = ( x 2 + y 2 )

Então

h ' = 2 y

E

g = e y 2 - x 2

Então

g ' = 2 y e y 2 - x 2

Agora a gente pode fazer a derivada

f y = 2 y e y 2 - x 2 + x 2 + y 2 2 y e y 2 - x 2

Simplificando

f y = 2 y e y 2 - x 2 ( 1 + x 2 + y 2 )

Passo 2

Beleza, agora a gente já tem nossas derivadas, os pontos interessantes vão acontecer quando elas forem iguais à 0. Então

f x = 2 x e y 2 - x 2 ( 1 - x 2 - y 2 ) = 0

f y = 2 y e y 2 - x 2 ( 1 + x 2 + y 2 ) = 0

Por f x tiramos que x = 0 implica f x = 0 . E por f y tiramos que y = 0 implica f y = 0 , substituindo y = 0 em f x temos

2 x e 0 2 - x 2 ( 1 - x 2 - 0 2 ) = 0

2 x e - x 2 ( 1 - x 2 ) = 0

Repare que para isso ser 0 temos duas possibilidades, ou 2 x e - x 2 = 0 o que implica x = 0 , ou 1 - x 2 = 0 , o que implica x = ± 1 .

Então daqui tiramos os pontos

0 ,   0 ,   0,1   e   0 , - 1

Agora vamos usar x = 0 e substituir em f y

2 y e y 2 - 0 2 1 + 0 2 + y 2 = 0

2 y e y 2 ( 1 + y 2 ) = 0

O único modo para isso ser 0 é com y = 0 .

Passo 3

Já temos nossos pontos de interesse, mas falta dizer se são máximos, mínimos ou pontos de sela, para isso a gente precisa da segunda derivada, vamos usar

D x , y = f x x ⋅ f x y - f x y 2

Podem ocorrer três casos:

  1. D ( a , b ) > 0   e   f x x a , b > 0 então f ( a , b ) é um mínimo local.
  2. D a , b > 0   e   f x x a , b < 0 então f ( a , b ) é um máximo local.
  3. D a , b < 0   então f ( a , b ) não é nem mínimo e nem máximo local.

Vamos calcular as segundas derivadas então

f x x = ∂ f x ∂ x

f x = 2 x e y 2 - x 2 ( 1 - x 2 - y 2 )

Agora derivamos isso em relação a x

f x x = ∂ 2 x e y 2 - x 2 ( 1 - x 2 - y 2 ) ∂ x = 2 e y 2 - x 2 1 - x 2 - y 2 1 - 2 x 2 - 2 x 2

A outra derivada que precisamos é

f y y = ∂ f y ∂ y

f y = 2 y e y 2 - x 2 ( 1 + x 2 + y 2 )

Derivando em relação a y

f y y = ∂ 2 y e y 2 - x 2 ( 1 + x 2 + y 2 ) ∂ y = 2 e y 2 - x 2 1 + x 2 + y 2 1 + 2 y 2 + 2 y 2

E a última derivada que precisamos é

f x y = ∂ f x ∂ y

ou f x y = ∂ f y ∂ x

f x = 2 x e y 2 - x 2 ( 1 - x 2 - y 2 )

Vamos derivar isso em relação a y

f x y = ∂ 2 x e y 2 - x 2 ( 1 - x 2 - y 2 ) ∂ y = 4 x y e x 2 + y 2 x 2 + y 2

Então

D x , y = 2 e y 2 - x 2 1 - x 2 - y 2 1 - 2 x 2 - 2 x 2 ⋅ 2 e y 2 - x 2 1 + x 2 + y 2 1 + 2 y 2 + 2 y 2 - 4 x y e x 2 + y 2 x 2 + y 2 2

Essa equação ficou grandinha né?

Passo 4

Vamos testar para o ponto 0,0

D 0 , 0 = 2 e 0 2 - 0 2 1 1 ⋅ 2 e 0 2 - 0 2 1 1

D 0,0 = 2 ⋅ 2

D 0,0 = 4

D 0 ,   0 > 0

Então temos que analisar f x x 0,0

f x x 0,0 = 2 e 0 2 - 0 2 1 1 = 2 > 0

Então 0 , 0 é um ponto de mínimo.

Agora o ponto 1 , 0

D 1 , 0 = 2 e - 1 1 - 1 1 - 2 - 2 ⋅ 2 e - 1 1 + 1 1

D 1 , 0 = - 4 e - 1 ⋅ 4 e - 1

D 1 ,   0 < 0

Logo é um ponto de sela.

Repare que isso é o mesmo para o ponto - 1 , 0

Passo 5

Agora só falta fazer o gráfico.

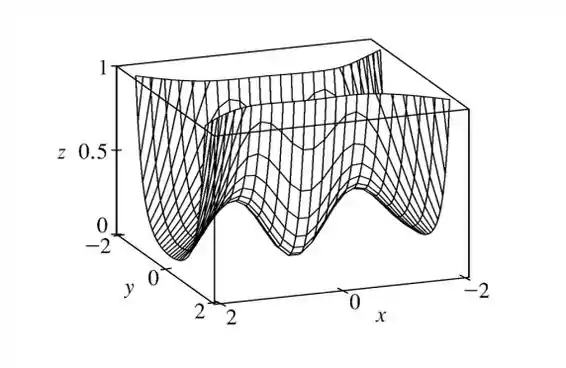
Resposta

Os pontos de sela são

1,0 ,   - 1 , 0

E o ponto de mínimo é

( 0,0 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

30. Determine a menor distância entre o ponto ( 2,1 , - 1 ) e o plano x + y - z = 1 .