Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 26

Utilize o Exercício 25 para achar o momento de inércia de um círculo de raio a com densidade constante em relação a um diâmetro (compare com o Exemplo 4 da Seção 15.5)

Passo 1

E aí, galerinha! Tudo certo?

A questão pede para calcularmos o momento de inércia de um círculo de raio a   em relação ao diâmetro utilizando o exercício 25, que traz as equações:

I x = - ρ 3 ∮ C y 3   d x                     I y = ρ 3 ∮ C x 3   d y

Como o círculo é simétrico, os dois momentos de inércia acima serão iguais. Como temos uma integral de linha, precisamos parametrizar nosso círculo em t e resolvermos a integral.

Vamos lá!

Passo 2

A fronteira do círculo pode ser representada por:

x 2 + y 2 = a 2

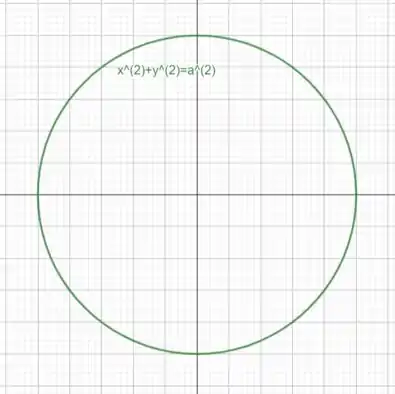
Então podemos parametrizar da seguinte forma:

x = a cos ⁡ t

y = a   s e n t

0 ≤ t ≤ 2 π

Do exercício 25, temos:

I x = - ρ 3 ∮ C y 3   d x

Aplicando nossa parametrização nessa relação:

I x = - ρ 3 ∫ 0 2 π sen ⁡ t 3 a   c o s t '

Assim, resolvendo a derivada dentro da integral:

I x = - ρ 3 ∫ 0 2 π a 3 s e n 3 t a - s e n t d t

Portanto,

I x = ρ 3 ∫ 0 2 π a 4 sen 4 ⁡ t d t

Tirando o que é constante e arrumando as coisas:

I x = a 4 ρ 3 ∫ 0 2 π sen 2 ⁡ t 2 d t

Vamos poder finalmente resolver nossa integral!

Passo 3

Agora vamos partir para integral.

I x = a 4 ρ 3 ∫ 0 2 π sen 2 ⁡ t 2 d t

Usando

sen 2 ⁡ t = 1 - cos ⁡ 2 t 2

Ficamos com:

I x = a 4 ρ 3 ∫ 0 2 π 1 - cos ⁡ 2 t 2 2 d t

Tirando a constante para fora:

I x = a 4 ρ 12 ∫ 0 2 π 1 - cos ⁡ 2 t 2 d t

Agora vamos abrir esse termo ao quadrado:

I x = a 4 ρ 12 ∫ 0 2 π 1 - 2 cos ⁡ 2 t + cos 2 ⁡ 2 t d t

Usando que

cos 2 ⁡ 2 t = cos ⁡ 2 t + 1 2

Substituímos:

I x = a 4 ρ 12 ∫ 0 2 π 1 - 2 cos ⁡ 2 t + 1 + cos ⁡ 4 t 2 d t

Agora já sabemos integrar. Fica assim ó:

I x = a 4 ρ 12 t - sen ⁡ 2 t + t 2 + sen ⁡ 4 t 8 0 2 π

Aplicando entre esses pontos:

I x = a 4 ρ 12 2 π + 2 π 2 = a 4 ρ 12 3 π

Logo,

I x = π a 4 ρ 4

Por simetria, os dois momentos de inércia serão iguais:

I y = I x = π a 4 ρ 4

Resposta

I x = I y = π a 4 ρ 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa e o centro de massa de um arame com formato da hélice x = t, y = cos ⁡ t, z = s e nt, 0 ≤ t ≤ 2 π, se a densidade em qualquer ponto for igual ao quadrado da sua distância do ponto à
(a) Escreva fórmulas semelhantes à Equação 4 para o centro de massa x C M ,y C M ,z C M de um arame fino com função densidade ρ x ,y ,z e forma da curva espacial C .(b) Determine o centro de massa de
Se um arame com densidade linear ρ x ,y está sobre uma curva plana C , seus momentos de inércia em relação aos eixos x e y são definidos por I x = ∫ C y 2ρ x ,y d s I y = ∫ C x 2ρ x ,y d s Determine o
Se um arame com densidade linear ρ x ,y ,z está sobre uma curva espacial C , seus momentos de inércia em relação aos eixos x , y e z são definidos por I x = ∫ C ( y 2 + z 2 ) ρ x ,y d s I y = ∫ C ( x
Se F é o campo vetorial do Exemplo 5, mostre que ∫ C F ⋅ d r = 0 para todo caminho fechado simples que não passe pela origem e nem a circunde. F x , y = - yi + xj x 2 + y 2