Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 28
Utilize uma ferramenta gráfica para encontrar os pontos críticos de com precisão de três casas decimais. Em seguida, classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfico, se houver.
Passo 1
A questão pede para acharmos os pontos críticos da função
Para o intervalo
Ou seja: Os pontos m��ximos, mínimos e de sela!
Se plotarmos esse gráfico em algum software (recomendo o GeoGebra) nós obtemos o seguinte
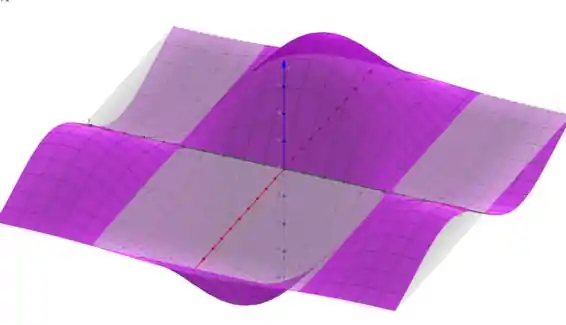
Em que, para o intervalo plotado, podemos observar quatro pontos críticos: Os dois morrinhos no eixo (vermelho) e os dois pontos de sela no eixo (verde)!
Assim, como a questão pediu para encontrarmos os pontos usando o gráfico, só precisamos identificá-los no software e classificá-los!
Em seguida a gente vai substituir o valor do máximo/mínimo global na função e encontrar os valores do gráfico!
Passo 2
Se verificarmos usando o software (no GeoGebra tem a ferramenta ponto, você pode selecionar ela e colocar sobre o local do ponto crítico) conseguimos os seguintes pontos críticos
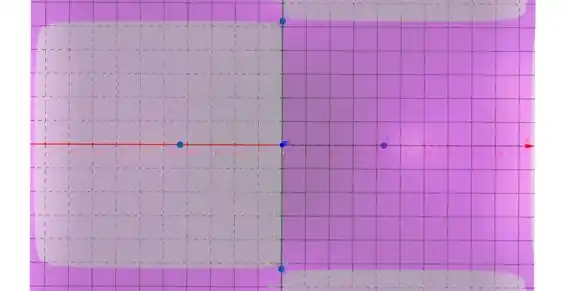
Onde é um ponto de máximo, é um ponto de mínimo e são pontos de sela!
Podemos garantir que estamos na precisão adequada encontrando os pontos críticos na base do cálculo, isto é, fazendo
De forma que
Da primeira equação, tiramos
Da segunda equação:
Da equação , encontramos . Já para a equação , achamos .
Por outro lado, de , achamos , enquanto para , achamos .
Assim, os pontos críticos realmente são
Passo 3
Por fim a questão pede para calcularmos os valores de máximo e mínimos desse gráfico, assim substituindo os pontos na função encontramos
Valor máximo da função
Valor mínimo da função
Resposta
Os pontos críticos são
Onde é um ponto de máximo, é um ponto de mínimo e são pontos de sela!
Valor máximo
Valor mínimo