Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 27
Utilize uma ferramenta gráfica para encontrar os pontos críticos de com precisão de três casas decimais. Em seguida, classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfico, se houver.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função:
E nosso objetivo é utilizar uma ferramenta gráfica para encontrar os pontos críticos de e classifica-los como máximos ou mínimos
Tem ideia de como fazemos isso?
A principio vamos usar uma ferramenta gráfica como por exemplo o Geogebra e determinar os pontos críticos.
Para classificar os pontos, vamos usar o teste da segunda derivada...
Calculamos as derivadas parciais de segunda ordem de .
Montamos a equação da matriz hessiana:
E analisamos os sinais de e .
Se e , o ponto é de mínimo, se o ponto é de máximo.
Se o ponto é sela e se não podemos afirmar nada.
Sacou? Bora começar!
Passo 2
Vamos começar plotando o gráfico de no Geogebra.
Pra isso só escrevermos a função no input do programa.
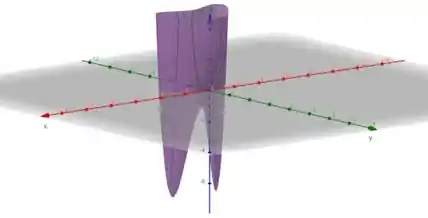
Ok... encontramos um gráfico de uma função que descreve um dente... 👀
A partir do seu gráfico podemos estimar três pontos críticos...
Tranquilo até aqui?
Passo 3
Agora vamos calcular as derivadas de para classificar esses pontos.
Nesse problema, nossa função é
Tomando as derivadas parciais de primeira ordem:
Para o teste da segunda derivada, tomamos as segundas derivadas:
Assim, o determinante hessiano será
Logo,
Show?
Passo 4
Vamos usar e para classificar nossos pontos.
Para , temos que
Como e nesses pontos, os pontos são de mínimo!
Já para , temos
Assim, esse ponto crítico é ponto de sela!
Pelo gráfico da função, não temos pontos máximos pois tende a quando ou crescem. Já os pontos mínimos globais são os pontos que estimamos anteriormente.
É isso! O que achou? Responde Aí!