Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.7 - Ex. 24
Utilize uma ferramenta gráfica como no Exemplo 4 (ou o Método de Newton ou um determinador de raízes) para encontrar os pontos críticos de com precisão de três casas decimais. Em seguida, classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfico.
Passo 1
Show de bola, galera...
Aqui nós temos a função
e queremos determinar os seus pontos críticos com o auxílio de uma ferramenta gráfica. Depois disso, classificaremos esses pontos entre máximo, mínimo e ponto de sela.
Os pontos críticos de são tais que .
Como saber se eles são pontos de máximo, mínimo ou sela?
Para uma variável nós usávamos o teste da derivada segunda. Para duas variáveis, vamos fazer algo parecido, mas da seguinte forma.
Seja o seguinte determinante
Então:
Além disso, pelo teorema de Clairaut: .
Portanto,
Os critérios são:
Se e , então é um mínimo local.
Se e , então é um máximo local.
Se , então não tem máximo nem mínimo local e é dito um ponto de sela.
Com isso nós já conseguimos resolver a questão.
Passo 2
Sendo
O seu gradiente será
Vamos calcular essas derivadas então:
Derivando com relação a :
Para o gradiente ser nulo, devemos ter
Multiplicando as duas equações por , temos
Podemos isolar na primeira e substituir na segunda equação, aí obteremos
e
Essas relações são satisfeitas com (.
Passo 3
Agora precisamos calcular as derivadas segundas nesse ponto crítico para poder classificá-lo.
Lembrando que
e
Então:
Agora podemos calcular essas derivadas no ponto crítico Temos três derivadas constantes, então só precisamos calcular efetivamente a seguinte:
Passo 4
Lembrando a definição de
Calculemos o sinal de e de para o respectivo ponto crítico:
– Para :
Como e , .
Passo 5
Show de bola, galera. Agora nós iremos apresentar o gráfico da função, só pra ver se o que calculamos está coerente. 
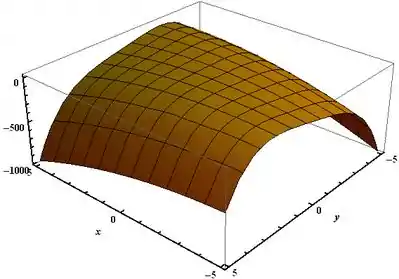
Veja que o gráfico tem concavidade para baixo, então faz sentido existir um ponto de máximo local.