Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 26
Utilize um gráfico e/ou curvas de nível para estimar os valores máximos e mínimos locais e pontos de sela da função. Em seguida, use o cálculo para achar esses valores precisamente.
Passo 1
Fala aí! tudo certinho?
Neste exercício, temos a função:
Queremos saber quais são os pontos onde essa função tem os maiores e os menores valores, e também os pontos onde ela muda de comportamento, chamados de pontos de sela.
Para isso, vamos usar duas ferramentas: os gráficos e o cálculo.
Como vamos resolver isso?
Primeiro, vamos desenhar as curvas de nível da função, que são as curvas que mostram os pontos que têm o mesmo valor da função e estimar os pontos extremos e sela.
Depois, vamos usar as derivadas parciais e o teste da segunda derivada para confirmar os nossos achados e calcular os valores exatos da função nesses pontos.
Pra isso, igualamo as derivadas parciais a zero e resolver o sistema de equações resultante, que nos dá os pontos críticos da função, onde ela pode ter máximos, mínimos ou pontos de sela.
Aplicamos o teste da derivada segunda, que nos permite classificar os pontos críticos de acordo com o sinal do determinante de uma matriz chamada hessiana, que contém as segundas derivadas da função.
Se e , o ponto é de mínimo, se o ponto é de máximo.
Se o ponto é de sela e se não podemos concluir nada.
Bora começar!
Passo 2
Show de bola, galera. Nesse nosso primeiro passo nós iremos apresentar as curvas de nível da função.
Em seguida, vamos calcular o que se pode observar dessas curvas, beleza? 
Representando o gráfico de em curvas de níveis dentro da região especificada no enunciado.
Temos:
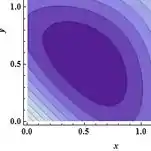
A partir do gráfico, podemos estimar um ponto máximo em torno de que é (aproximadamente) o centro da parte mais escura do gráfico.
E o ponto mínimo em pois é onde a cor parece mais fraca.
Tranquilo até aqui?
Passo 3
Basicamente precisaremos calcular os seguintes valores: , , , e .
Vamos lá?
Se
Calculando as derivadas de primeira ordem...
A partir dessas derivadas, derivamos novamente para montar a matriz hessiana.
Montando a matriz hessiana, temos:
Show?
Passo 4
Como vimos no passo 1, calculamos os pontos críticos fazendo e .
A partir desse sistema, igualando as duas equações, podemos determinar...
Isso implica que , substituindo isso na primeira equação, obtemos:
Essa equação representa um conjunto de valores...
Os valores de , e estão fora do nosso domínio, então podemos desconsidera-los.
Com isso temos apenas um ponto crítico...
Bacana, não é?
Passo 5
Calculemos o sinal de e de para nosso ponto critico para classifica-lo como vimos no passo 1:
– Para :
Substituindo em .
Como e , concluímos que .
Maravilha!
Passo 6
Ainda não acabou! Temos que analisar também os limites da região...
Como já vimos o gráfico da função, sabemos que em vamos ter um mínimo local.
Então vamos calcular a imagem da função nesse ponto e aproveitar para calcular a imagem da função em .
Em , temos:
Em :
E fim! O que achou? Responde Aí!