Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 23

Utilize um gráfico e/ou curvas de nível para estimar os valores máximos e mínimos locais e pontos de sela da função. Em seguida, use o cálculo para achar esses valores precisamente.

f x , y = x 2 + y 2 + x - 2 y - 2

Passo 1

Show de bola, galera. Nesse nosso primeiro passo nós iremos apresentar o gráfico da função. Em seguida, vamos calcular o que se pode observar do gráfico, beleza?

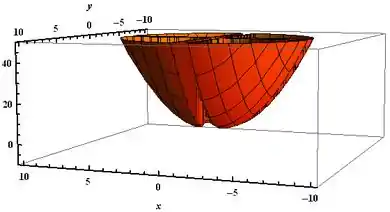
Passo 2

Show de bola, galera....Vamos às contas...

Basicamente precisaremos calcular os seguintes valores: f x , f y , f x x , f x y   e   f y y . E aí, meus amigos, não tem mistério! No Passo 3 calcularemos os pontos críticos da função ao fazer f x = 0   e   f y = 0 . No Passo 4 usaremos o Teste da Derivada Segunda ao calcularmos D = f x x f x y f y x f y y e avaliarmos o seu sinal juntamente com o sinal de f x x .

Vamos lá?

Passo 3

Calculemos os pontos críticos de f ( x , y ) da seguinte forma:

∂ f ∂ x = 0 ∂ f ∂ y = 0   ∴   2 x - 2 x - 3 y - 2 = 0 2 y - 2 x - 2 y - 3 = 0   ∴   x 4 = y - 2 y 4 = x - 2 ⇒ P o n t o s   c r í t i c o s 1,1 , 1 , - 1 , - 1,1 , - 1 , - 1

Passo 4

Calculemos o sinal de D = f x x f x y f y x f y y = 2 + 6 x - 4 y - 2 4 x - 3 y - 3 4 x - 3 y - 3 2 + 6 x - 2 y - 4 e de f x x para os respectivos pontos críticos:

– Para x c , y c = 1 , 1 :

D = 2 + 6 x - 4 y - 2 4 x - 3 y - 3 4 x - 3 y - 3 2 + 6 x - 2 y - 4 1,1 = 8 4 4 8 = 48 > 0

f x x 1,1 = 8 > 0

Como D > 0 e f x x > 0 , concluímos que x c , y c = ( 1,1 )  é um ponto de mínimo local .

– Para x c , y c = 1 , - 1 :

D = 2 + 6 x - 4 y - 2 4 x - 3 y - 3 4 x - 3 y - 3 2 + 6 x - 2 y - 4 1 , - 1 = 8 - 4 - 4 8 = 48 > 0

f x x 1 , - 1 = 8 > 0

Como D > 0 e f x x > 0 , concluímos que x c , y c = ( 1 , - 1 )  é um ponto de mínimo local .

– Para x c , y c = - 1 , 1 :

D = 2 + 6 x - 4 y - 2 4 x - 3 y - 3 4 x - 3 y - 3 2 + 6 x - 2 y - 4 - 1,1 = 8 - 4 - 4 8 = 48 > 0

f x x - 1,1 = 8 > 0

Como D > 0 e f x x > 0 , concluímos que x c , y c = ( - 1,1 )  é um ponto de mínimo local .

– Para x c , y c = - 1 - , 1 :

D = 2 + 6 x - 4 y - 2 4 x - 3 y - 3 4 x - 3 y - 3 2 + 6 x - 2 y - 4 - 1 , - 1 = 8 4 4 8 = 48 > 0

f x x - 1 , - 1 = 8 > 0

Como D > 0 e f x x > 0 , concluímos que x c , y c = ( - 1 , - 1 )  é um ponto de mínimo local .

Resposta

( 1,1 )   é   u m   p o n t o   d e   m í n i m o   l o c a l ( 1 , - 1 )   é   u m   p o n t o   d e   m í n i m o   l o c a l ( - 1,1 )   é   u m   p o n t o   d e   m í n i m o   l o c a l ( - 1 , - 1 )   é   u m   p o n t o   d e   m í n i m o   l o c a l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que f x ,y = x 2 y e - x 2 - y 2 tem valores máximos em ± 1 , 1 2 e valores mínimos em ± 1 ,- 1 2 . Mostre também que f tem infinitos outros pontos críticos e que D = 0 em cada um deles. Quais
Selecione os candidatos a extremos locais, sendo f (x , y) = 2 x^2 + y^2 - 2 x y + x - y
Selecione os candidatos a extremos locais, sendo f x , y = 3. x 2 - y 2 + x y + 5