Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 2
Utilize a Regra do Ponto médio para estimar a integral do exercício 1.
Passo 1
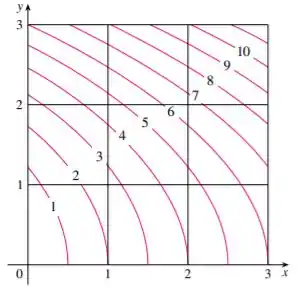
E aí meus queridxs, tudo bom com vocês? Como o exercício cita a questão vamos descrevê-la aqui porque precisaremos da imagem da mesma para resolver essa questão aqui. A questão diz o seguinte: “A figura mostra o mapa de contorno de no quadrado . Utilize uma soma de Riemann de nove termos para estimar o valor de . Tome os pontos de amostragem como os cantos superiores direitos dos quadrados.”
Passo 2
Para estimar essa integral nesse problema vamos utilizar o método do ponto médio que é dado pela seguinte fórmula
Como no exercício , temos e vamos pegar cada um desses 9 quadrados com área para nossa resolução. Usando o mapa de contorno para estimar o valor de no centro de cada quadradinho desses, temos para o somatório
Do exercício anterior a gente já aprendeu como encontrar os valores estimados para as funções nos pontos indicados (vamos utilizar as linhas rosa do nosso mapa). Sendo assim vamos ter
Pronto, tá resolvido nosso exercício sem muito problema.
