Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 62

Encontre o valor médio de f na região D .

f x , y = x sen ⁡ y ,     D   é   l i m i t a d o   p e l a s   c u r v a s   y = 0 ,   y = x 2   e   x = 1 .

Passo 1

Falaa, pessoal, tudo bem?

Vamos ver o que essa questão pede.

Ela quer que a gente encontre o valor médio da função f em uma região que ela deu. O valor médio de f é dado pela expressão:

f m é d i o = 1 A D ∬ D f x , y d A

Onde A ( D ) é a área da região D .

Então pra calcular o f m é d i o a gente começa vendo quem é D , pra conseguirmos calcular a área e a integral ∬ D f x , y d A . No final, é só juntar tudo na fórmula.

Passo 2

Vamos esboçar a região D :

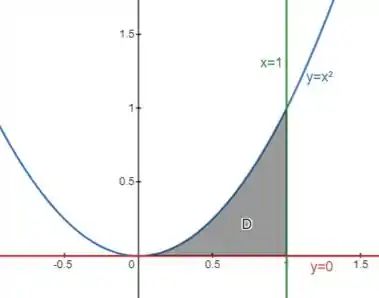
A região D então é definida com esses limites:

0 ≤ x ≤ 1

0 ≤ y ≤ x 2

Então:

D = x , y | 0 ≤ x ≤ 1 ,   0 ≤ y ≤ x 2

Pra calcular a área de D a gente pode usar integral simples pra encontrar a área embaixo de y = x 2 entre 0 e 1 :

A D = ∫ 0 1 x 2 d x =

= x 3 3 0 1 = 1 3

Passo 3

Agora vamos para a integral dupla:

∬ D x sen ⁡ y d A = ∫ 0 1 ∫ 0 x 2 x sen ⁡ y d y d x =

Primeiro integrando em função de y :

= ∫ 0 1 ∫ 0 x 2 x sen ⁡ y d y d x =

Como consideramos x constante:

= ∫ 0 1 x ∙ - cos ⁡ y 0 x 2 d x =

= ∫ 0 1 x ∙ - cos ⁡ x 2 + cos ⁡ 0 d x =

Como cos ⁡ 0 = 1 :

= ∫ 0 1 x ∙ - cos ⁡ x 2 + 1 d x

Passo 4

Para resolver a integral em função de x primeiro vamos separar em duas integrais:

∫ 0 1 x ∙ - cos ⁡ x 2 + 1 d x = - ∫ 0 1 cos ⁡ x 2 ∙ x d x + ∫ 0 1 x d x =

Pra primeira integral, nós vamos usar a substituição u = x 2 :

d u = 2 x d x

u 0 = 0

u 1 = 1

Então:

- ∫ 0 1 cos ⁡ x 2 ∙ x d x ⏟ 1 2 d u + ∫ 0 1 x d x =

= - ∫ 0 1 1 2 cos ⁡ u d u + ∫ 0 1 x d x =

Agora podemos integrar em u e x :

= - 1 2 sen ⁡ u 0 1 + x 2 2 0 1 =

= - 1 2 sen ⁡ 1 - sen ⁡ 0 + 1 2 2 - 0 2 2 =

Colocando 1 2 em evidência:

= 1 2 - sen ⁡ 1 + 0 + 1 - 0

⇒ ∬ D x sen ⁡ y d A = 1 2 1 - sen ⁡ 1

Passo 5

Pra achar o valor médio então, só falta colocarmos tudo na fórmula:

f m é d i o = 1 A D ∬ D f x , y d A =

= 1 1 3 ∙ 1 2 1 - sen ⁡ 1

E encontramos:

f m é d i o = 3 2 ( 1 - sen ⁡ 1 )

Resposta

f m é d i o = 3 2 1 - sen ⁡ 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Propriedade 11 para estimar o valor da integral. ∬ S 4 - x 2 y 2 d A ,S = x , y | x 2 + y 2 ≤ 1 ,x ≥ 0
A figura mostra o mapa de contorno de f no quadrado R = 0,3 × 0,3 . Utilize uma soma de Riemann de nove termos para estimar o valor de ∫ ∫ R f x , yd A . Tome os pontos de amostragem como os cantos su
Utilize a Regra do Ponto médio para estimar a integral do exercício 1.
Se D é uma região limitada pelas curvas y = 1 - x 2ey = e x , determine o valor aproximado da integral ∫ ∫ D y 2d A . (Utilize uma ferramenta gráfica para estimar os pontos de intersecção das curvas.)