Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 1
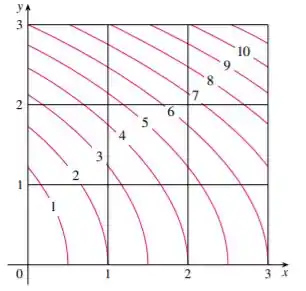
A figura mostra o mapa de contorno de no quadrado . Utilize uma soma de Riemann de nove termos para estimar o valor de . Tome os pontos de amostragem como os cantos superiores direitos dos quadrados.
Passo 1
E aí meus queridxs, tudo bom? Se liguem só que essa questão é bem rapidinha, porém, precisa de bastante atenção para conseguir entender toda a resolução. Pois bem, a gente consegue ver no mapa de contorno quadrado que ele está dividido em 9 pequenos outros quadrados, cada um com área Então, nós podemos aproximar nossa integral
Utilizando a soma de Riemann com e a amostra aponta os cantos superiores direitos de cada quadrado, sendo assim teremos
Mas o que é essa tal soma de Riemann?
Um exemplo de uma aplicação de uma soma de Riemmen é o cálculo de uma área pela soma várias figuras que juntas fornecerão uma estimativa para o valor dessa área.
Passo 2
Nosso somatório pode ser, então, escrito como
Beleza, nosso problema está quase resolvido só precisamos estimar o valor da função para esses pontos, mas como vamos fazer isso?
Calma pequeno gafanhoto que aqui a gente dá um jeito. Veja que pois cada quadrado menor possui de área. Veja o ponto
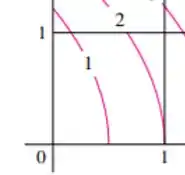
Sua intersecção está entra a linha e a linha (rosa). De modo que uma estimativa razoável para seu valor é Siga o mesmo procedimento para os outros valores e encontrará:
Pronto, tá resolvido nosso exercício sem muitos problemas.