Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.1 - Ex. 16
A equação de Von Bertalanffy afirma que a taxa de crescimento em comprimento de um peixe individual é proporcional à diferença entre o comprimento atual e o comprimento assintótico (em centímetros).
a) Escreva uma equação diferencial que expresse essa idéia.
b) Faça um esboço do gráfico de uma solução de um problema típico de valor inicial para esta equação diferencial.
Passo 1
a) Então pessoal, o enunciado está falando de taxa de crescimento. Sempre que a palavra taxa for associada a alguma dependência, significa que estamos falando de derivada! Escrevendo uma equação diferencial tendo as características descritas, obteremos:
Na equação que escrevemos é a constante de proporcionalidade da equação diferencial, no qual deve ser maior do que zero, claro! Ademais, fica bem claro que depende de .
Passo 2
b) Antes de esboçarmos o gráfico devemos resolver essa equação diferencial, certo? De início o que precisamos fazer é separar essas variáveis que estão juntas, se liga:
Integrando ambos os membros, teremos:
Do lado esquerdo da equação, podemos fazer:
Aqui vale ressaltar que se comporta como uma constante, por isso some na derivação. Substituindo, teremos:
Unindo as constantes e substituindo novamente, teremos:
Passo 3
Tudo bem, resolvemos a integral, agora o que precisamos fazer é isolar . Aplicando a propriedade geral de logaritmos:
Isolando :
Se plotarmos o gráfico dessa função, obteremos algo do tipo:
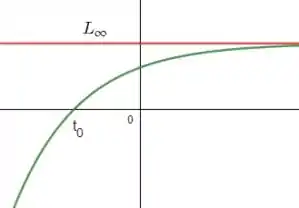
Ter uma assíntota horizontal faz total sentido, uma vez que um peixe não pode crescer indefinidamente, não é mesmo? Sendo assim, o resultado nos parece aceitável! 😊
Resposta
a)
b)
