Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.2 - Ex. 3
Utilize uma tabela de valores numéricos de para perto da origem para conjecturar sobre o limite de quando . Em seguida, explique por que sua conjectura está correta.
Passo 1
Pessoal, primeiro vamos fazer uma tabela com os valores de para vários valores de perto da origem:
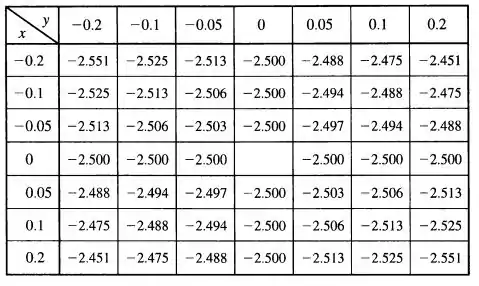
Como a tabela mostra, os valores de parecem se aproximar de . Então vamos conjecturar que:
Passo 2
Show! Agora vamos tentar provar que nossa conjectura é verdadeira. Como é uma função racional, ela é contínua em seu domínio, e faz parte desse domínio. Então podemos substituir diretamente para calcular o limite:
Resposta
Exercícios de Livros Relacionados
Determine se underset((x , y) - (x_0 , y_0))(lim) f (x , y) existe nos seguintes casos:(c) f (x , y) = (x y)/(sqrt(x^2 + y^2)) , (x_0 , y_0) = (0 , 0)
Determine se underset((x , y) - (x_0 , y_0))(lim) f (x , y) existe nos seguintes casos:(a) f (x , y) = (x^2 y^2)/(x^2 + y^2) , (x_0 , y_0) = (0 , 0)
Encontre os limites nos Exercícios 1-12.
Encontre os limites nos Exercícios 1-12.
Encontre os limites nos Exercícios 1-12.