Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 13

Variação catastrófica no crescimento logístico. Suponha que uma população saudável de algumas espécies cresça em um ambiente limitado e que a população atual P 0   esteja bastante próxima da capacidade de carga M 0 . Você pode imaginar uma população de peixes vivendo em um lago de água doce em uma área selvagem. De repente, uma catástrofe, tal como a erupção vulcânica do Monte St. Helens, contamina o lago e destrói uma parte significativa do alimento e do oxigênio dos quais os peixes dependem. O resultado é um novo ambiente com uma capacidade de carga M 1 , consideravelmente menor do que M 0 e, de fato, menor do que a população atual P 0 . Partindo de algum momento antes da catástrofe, esboce uma curva "antes e depois" que mostre como a população de peixes responde à mudança no ambiente.

Passo 1

A questão deseja que façamos um gráfico genérico esboçando a situação problema que, nesse caso, é o crescimento da população de peixes em 2 momentos. No primeiro deles temos a população apresentando um crescimento até uma cota superior M 0 , no entanto, em um determinado t temos uma catástrofe que faz com que haja um decrescimento até uma cota M 1 que agora é muito inferior ao valor que a função atingiria anteriormente. Dessa forma, nosso gráfico de “antes e depois” fica da seguinte forma:

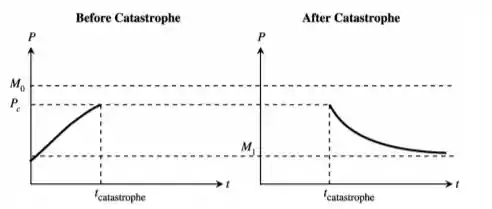
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

17. O calor transferido de um corpo para seu ambiente por radiação, baseado na lei de StefanBoltzmann,5 é descrito pela equação diferencial d u d t = - α u 4 - T 4 em que u(t) é a temperatura absoluta
17. O calor transferido de um corpo para seu ambiente por radiação, baseado na lei de StefanBoltzmann,5 é descrito pela equação diferencial d u d t = - α u 4 - T 4 em que u(t) é a temperatura absoluta
14. Suponha que determinada população tem uma taxa de crescimento que varia com o tempo e queessa população satisfaz a equação diferencialdy/dt =(0,5 + sen t)y/5.(a) Se y(0) = 1, encontre (ou estime)
15 . Suponha que determinada população satisfaz o problema de valor inicialdy/dt = r(t)y – k, y(0) = y0,em que a taxa de crescimento r(t) é dada por r(t) = (1 + sen t)/5, e k representa a taxa predató
15 . Suponha que determinada população satisfaz o problema de valor inicialdy/dt = r(t)y – k, y(0) = y0,em que a taxa de crescimento r(t) é dada por r(t) = (1 + sen t)/5, e k representa a taxa predató