Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 17-b
17. O calor transferido de um corpo para seu ambiente por radiação, baseado na lei de StefanBoltzmann,5 é descrito pela equação diferencial
em que u(t) é a temperatura absoluta (em graus Kelvin) do corpo no instante t, T é atemperatura absoluta do ambiente, e α é uma constante que depende dos parâmetros físicos docorpo. No entanto, se u for muito maior do que T, as soluções da Eq. (i) podem ser bemaproximadas por soluções da equação mais simples
Suponha que um corpo, a uma temperatura inicial de 2000°K, está em um meio à temperaturade 300°K e que α = 2,0 × 10–12 °K–3/s.(a) Determine a temperatura do corpo em um instante qualquer resolvendo a Eq. (ii).(b) Faça o gráfico de u em função de t.(c) Encontre o instante τ no qual u(τ) = 600, ou seja, o dobro da temperatura ambiente. Até esseinstante, o erro ao usar a Eq. (ii) para aproximar as soluções da Eq. (i) não é maior do que 1%.
Passo 1
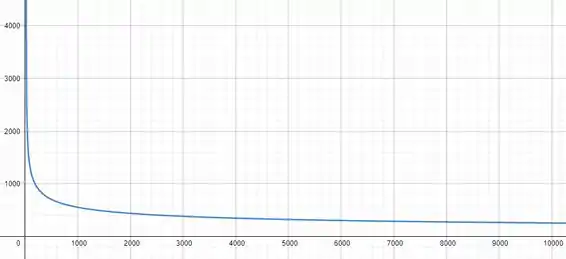
O grafico de
Pode ser observado abaixo, como podemos ver, como a constante que multiplica a nossa função é muito pequena , nossa função vai decaindo mas bem lentamente
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)