Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 66
A velocidade de uma partícula movendo-se ao longo do eixo é medida em intervalos de 5 segundos durante 40 segundos, e a função velocidade está modelada por uma curva lisa que passa pelos pontos dados, conforme a figura a seguir. Use esse modelo em cada parte.
(a) A partícula tem aceleração constante? Explique seu raciocínio.
(b) Há algum intervalo de 15 segundos durante o qual a aceleração é constante? Explique seu raciocínio.
(c) Estime a distância percorrida pela partícula de a .
(d) Estime a velocidade média da partícula no período de 40 segundos.
(e) A partícula está diminuindo sua velocidade alguma vez durante os 40 segundos? Explique seu raciocínio.
(f) Há informação suficiente para determinar a coordenada da partícula em ? Se houver, encontre-a. Se não, explique qual a informação adicional necessária.
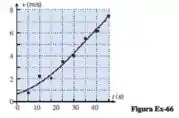
Passo 1
A primeira pergunta que temos é se a aceleração é constante, diante disso, respondemos que não pois a curva de velocidade não é uma linha reta!!
Para o item (b), podemos ver pelo gráfico que entre o intervalo de a reta não possui curvas, portanto a aceleração será constante.
Passo 2
Para o item (c), podemos usar a fórmula do movimento uniformemente acelerado:
Como a aceleração é constante, então
Portanto, a distância percorrida pela partícula de a é .
Usando esse valor, calculamos a velocidade média da partícula no período de 40 segundos para o item (d):
Passo 3
Para o item(e), a partícula não está diminuindo sua velocidade alguma vez durante os 40 segundos, pois a velocidade é positiva e a aceleração nunca é negativa.
E, por fim, para o item (f), precisa da posição a qualquer momento (por exemplo, ).
Resposta
(a) não pois a curva de velocidade não é uma linha reta.
(b)
(c)
(d)
(e) não, pois a velocidade é positiva e a aceleração nunca é negativa.
(f) precisa da posição a qualquer momento (por exemplo, ).