Verdadeiro/Falso
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta
34) A imagem da função arco tangente é o intervalo:
Passo 1
Fala povo, tudo bem? Olha, a gente quer a imagem de:
Como arco tangente é uma função inversa trigonométrica, que quer dizer que é igual ao arco cuja tangente é , ao invertermos a inversa, achamos a trigonométrica original! Ou seja:
Lendo essa função, estamos dizendo que é igual a tangente do arco . A mesma coisa de antes, certo? Só falamos ao contrário. Agora, se:
Então:
Só que se olharmos bem pro círculo trigonométrico:
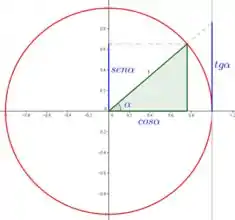
Vemos que se o arco fica muito pertinho de , a tangente explooode lá pro infinito e se o arco fica muito pertinho de , o mesmo acontece, só que pra valores infinitamente grandes e negativos:
E bem galera, isso aí é uma verdade! Olhando pro próprio círculo trigonométrico vemos que uma tangente pode ser tão infinitamente grande ela queira! A afirmativa então é verdadeira! Pra fins ilustrativos, olha só esses gráficos:
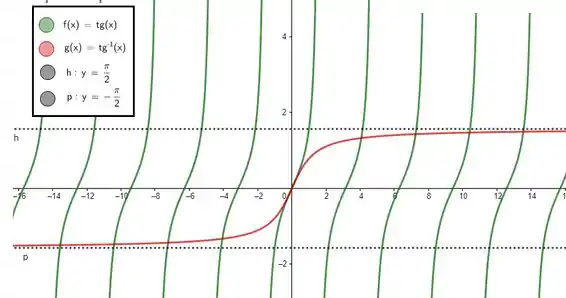
Resposta
Verdadeiro