Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 50a
Enfocando conceitos
A função é definida como sendo a inversa da função cotangente restrita:
E a função é definida como sendo a inversa da função cossecante restrita:
Use essas definições em todos os exercícios subsequentes que envolverem essas funções.
Mostre que:
Passo 1
Fala galera, tudo bem? Então, bora começar com essa letra , ok? Pra início de conversa, vamos definir, na letra , que:
Como a questão diz que arco cotangente é a inversa da cotangente limitada pra , acabamos pegando a imagem de . Afinal, quando invertemos uma função, domínio e imagem trocam de lado. Logo:
Show, agora vamos lembrar o seguinte: é um arco, é um valor de cotangente. O enunciado já diz pra gente que a função é definida por partes, com e . Então, pra facilitar a nossa vida, seja:
E tendo o círculo trigonométrico:
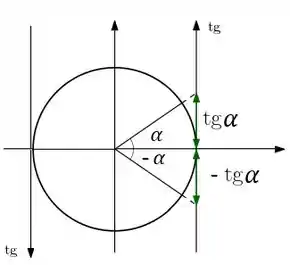
Vemos que e são positivas no primeiro quadrante e negativas no segundo. Como , nem vamos nos preocupar com os outros quadrantes, ok? Depois desse panorama geral, nossos próximos passos vão ser olhar pros casos:
E ver como podemos inverter em cada um desses casos. Partiu?
Passo 2
Se , temos uma cotangente positiva e logo:
Nesse caso, partindo de:
Podemos inverter a função, ficando com:
Invertendo a função de novo, achamos:
Agora, se , temos cotangente negativa. O intervalo do arco será o segundo quadrante:
E nesse caso, partindo de:
Podemos inverter a função, ficando com:
E dessa vez temos um problema ao inverter, temos que achar um arco negativo! Pela simetria do círculo trigonométrico vemos que:
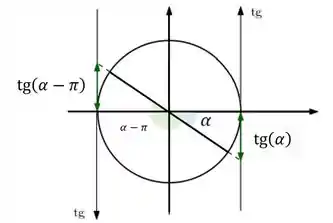
Analogamente, temos que:
Logo:
Invertendo a função de novo, achamos:
Show, só juntar agora as duas definições e achamos:
Ufa! Cabamos
Resposta
Provado no desenvolvimento