Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 4.2 - Ex. 35

Verifique por substituição direta que a fórmula (4) satisfaz a equação (2)

Passo 1

Salveee, vamos pra mais um probleminha?

Queremos provar que a fórmula (4) do seu livro satisfaz a equação (2)

Ta, vamos lembrar quem é (4) e quem é (2)

A fórmula (4) do seu livro é essa aqui:

y 2 x = y 1 x ∫ e - ∫ P x d x y 1 2 x   d x     ( 4 )

E a equação (2) é essa:

y ' ' + P x y ' + Q x y = 0     ( 2 )

Aí precisamos substituir a equação (4) no lugar de y na equação (2)

Vamos lá?

Passo 2

Pra começar, temos que encontrar a primeira e a segunda derivada da equação (4), pra aí sim substituirmos ela na equação (2).

Então bora:

y 2 x = y 1 x ∫ e - ∫ P x d x y 1 2 x   d x

Derivando uma vez (usando a regra do produto):

y 2 x ' = y 1 ' x ∫ e - ∫ P x d x y 1 2 x   d x + y 1 . ∫ e - ∫ P x d x y 1 2 x   d x '

A derivada da integral é a própria função lá de dentro, então:

y 2 x ' = y 1 ' x ∫ e - ∫ P x d x y 1 2 x   d x + y 1 . e - ∫ P x d x y 1 2 x

Agora vamos derivar mais uma vez para encontrarmos a segunda derivada

No primeiro termo (laranja), aplicamos regra do produto

No segundo termo (roxo), aplicamos regra da cadeia e do quociente

y 2 x ' ' = y 1 ' ' x . ∫ e - ∫ P x d x y 1 2 x   d x + y 1 ' . e - ∫ P x d x y 1 2 x + e - ∫ P x d x ' . y 1 x - e - ∫ P x d x . y 1 x ' y 1 2 ( x )

y 2 x ' ' = y 1 ' ' x . ∫ e - ∫ P x d x y 1 2 x   d x + y 1 ' y 1 2 ( x ) . e - ∫ P x d x + - P x e - ∫ P x d x . y 1 x - e - ∫ P x d x . y 1 x ' y 1 2 ( x )

y 2 x ' ' = y 1 ' ' x . ∫ e - ∫ P x d x y 1 2 x   d x + y 1 ' y 1 2 ( x ) . e - ∫ P x d x + - P x e - ∫ P x d x . y 1 x y 1 2 ( x ) + - e - ∫ P x d x . y 1 x ' y 1 2 ( x )

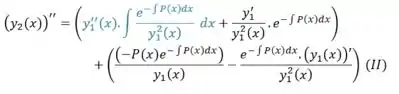
Belezinha, já temos a primeira e a segunda derivada, agora é só substituir ;)

Passo 3

A equação (2) é

y ' ' + P x y ' + Q x y = 0     ( 2 )

Vamos substituir a parte laranja de ( I ) em y ' , a parte azul de ( I I ) em y ' ' e a equação ( 4 ) em y :

y 1 ' ' x . ∫ e - ∫ P x d x y 1 2 x   d x + P x y 1 ' x . ∫ e - ∫ P x d x y 1 2 x   d x + Q x y 1 x ∫ e - ∫ P x d x y 1 2 x   d x = 0

Colocando ∫ e - ∫ P x d x y 1 2 x   d x em evidência:

∫ e - ∫ P x d x y 1 2 x   d x . y 1 ' ' x + P x . y 1 ' x + Q x . y 1 x = 0

Mass temos que y 1 ' ' x + P x . y 1 ' x + Q x . y 1 x = 0 , então, de fato, a igualdade acima vale 0 hehehe ta provadooo

Resposta

D e m o n s t r a ç ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. y ' ' + 2 y ' + y = 0 ; y 1 = x e
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. x 2 y ' ' + 2 x y ' - 6 y = 0 ;y 1
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. 6 y ' ' + y ' - y = 0 ;y 1 = e x 3
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. x 2 y ' ' - 7 x y ' + 16 y = 0 ;y
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. x y ' ' + y ' = 0 ;y 1 = ln ⁡ x