Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.3 - Ex. 46
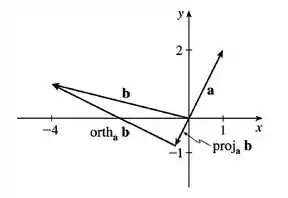
Para os vetores do Exercício 36, determine e ilustre esboçando os vetores e .
Passo 1
Sabemos que
E, lá do exercício 36, nós calculamos que
Assim,
Passo 2
Agora é só a gente esboçar todas esses vetores no mesmo desenho.
Vou organizar todos eles aqui e depois a gente desenha:
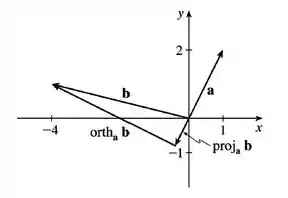
Graficamente dá pra gente entender bem melhor o que essas coisas significam né? é a projeção do vetor no vetor , por isso o vetor fica na mesma direção do vetor e é a projeção perpendicular do vetor no vetor , por isso esse vetor fica na direção perpendicular a do vetor .
Resposta
Exercícios de Livros Relacionados
Cordas de 3 m e 5 m de comprimento são atadas à decoração natalina suspensa sobre uma praça. A decoração tem massa de 5 kg. As cordas, atadas em diferentes alturas, fazem ângulos de 52 ° e 40 ° com a
Velocidades têm módulo, direção e sentido, sendo portanto vetores. O módulo de uma velocidade é chamado velocidade escalar. Suponha que esteja ventando na direção N 45 ° W a uma velocidade de 50 km/h.
Se r =x , y , z e r 0 =x 0 , y 0 , z 0 , descreva o conjunto de todos os pontos ( x , y , z ) tal que r - r 0 = 1
A figura 16 fornece uma demonstração geométrica da Propriedade 2 dos vetores. Use as componentes para dar uma demonstração algébrica desse fato no caso n = 2 .
Se A ,B e C são vértices de um triângulo, determine A B → + B C → + C A → .