Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 8
Se os vetores da figura satisfizerem e o que é ?
Passo 1
Bom, se , podemos escrever .
Os vetores formam um triângulo retângulo, assim:
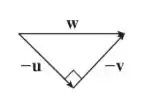
Então, podemos aplicar teorema de Pitágoras aqui:
Agora é só desenvolver...
Prontinho😊
Resposta
Exercícios de Livros Relacionados
Use o processo de ortogonalização de Gram-Schmidt para encontrar uma base ortonormal para o subespaço de R 4 que tem como base { ( 1,1 , - 1,0 ) , ( 0,2 , 0,1 ) , ( - 1,0 , 0,1 ) } .
Seja S = { W 1 ,. . . ,W k } uma base ortogonal de um subespaço W de R n . Mostre que todo vetor V de W pode ser escrito como V = V ⋅ W 1 | | W 1 | | 2 W 1 + V ⋅ W 2 | | W 2 | | 2 W 2 +. . .+ V ⋅ W k
Encontre um subconjunto com o maior número possível de vetores ortonormais no conjunto solução do sistema homogêneo
Seja W um subespaço de R n . Mostre que o conjunto de todos os vetores ortogonais a todos os vetores de W é um subespaço de R n . Este subespaço é chamado de complemento ortogonal de W e denotado por
Use o processo de ortogonalização de Gram-Schmidt para encontrar uma base ortonormal de R 3 que tem como base { ( 1,1 , 1 ) , ( 0,1 , 1 ) , ( 1,2 , 3 ) } .