Encontre um subconjunto com o maior número possível de vetores ortonormais no conjunto solução do sistema homogêneo

Primeira coisa que nós precisamos fazer é simplificar este sistema o máximo possível, portanto, vamos escalonar a matriz aumentada que representa este sistema de equações, beleza? A matriz é tal que:

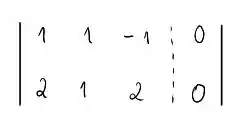
No escalonamento, a primeira coisa é identificar o pivô (primeiro termo da primeira coluna), como ele já é 1, não precisamos fazer nada nele. Então de cara já podemos começar eliminando o termo que resta na coluna 1. Para isso vamos subtrair da linha 2 a primeira linha multiplicada por 2, obtendo:

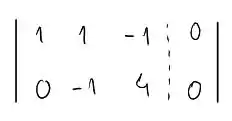
Para continuar o escalonamento, devemos multiplicar a segunda linha por -1, de forma que temos:

Agora, podemos eliminar o termo que sobra na segunda coluna (não é necessário, mas simplifica). Apenas fazendo a primeira linha menos a segunda, temos:

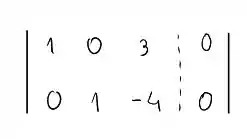
Isso é o mais simples que podemos deixar, agora podemos identificar que nosso sistema se simplifica ao seguinte:

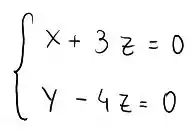
Vamos continuar a nossa questão agora! Belezinha?

Nós temos 3 parâmetros livres e apenas duas equações, portanto, vamos escolher um parâmetro qualquer como . E escrever o seguinte:

E portanto, temos a seguinte relação:

Esta expansão pode ser expandida em termos do parâmetro da seguinte maneira:

De forma que nossa base pode ser identificada como , ele é L.I. já que é um único vetor não nulo, vamos apenas verificar se é normalizado, beleza?

Um vetor normalizado pode ser obtido fazendo:

Portanto, usando a definição (2), temos:

e aplicando (3), temos:

Aí está nossa base ortonormal, te vejo na próxima! Tchauzinho!