Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 35b
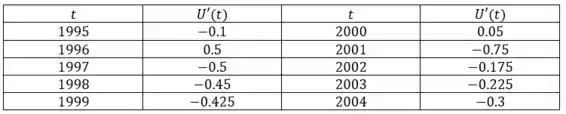
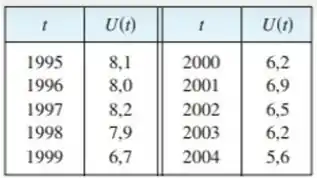
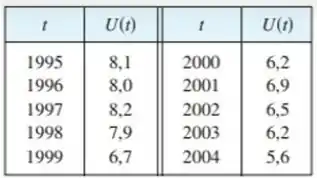
A taxa de desemprego varia com o tempo. A tabela dá a porcentagem de desempregados na força de trabalho australiana em meados de 1995 a 2004.
b) Construa uma tabela de valores estimados para .
Passo 1
Fala aí, pessoal. Tudo belezinha com vocês?
Bom, a questão deu pra gente uma tabela que representa a porcentagem de desempregados na força de trabalho australiana em meados de 1995 a 2004, e pediu pra gente construir uma tabela de valores estimados para .
Bom galera, a derivada sempre representa a inclinação de um função em um ponto. Olhar para essa derivada pode nos ajudar a entender o que está acontecendo ano a ano com esse percentual.
Quanto maior a derivada (inclinação) mais rapidamente a função está crescendo, por exemplo.
Então, bora construir essa tabela de .
Sendo a derivada dada pela definição:
Então vamos usar essa relação, aí.
Vem comigo que te mostro como no passo a passo.
Passo 2
Beleza, então a gente pode calcular a derivada estimada em cada um dos anos entre e , usando as informações da tabela da função.
Para 1995, fazemos:
Passo 3
E para os outro anos, a gente pega uma média entre a aproximação por dois lados, isso vai fazer como que tenhamos uma melhor aproximação para .
Assim, para 1996, temos os pares (1995 e 1996) e (1996 e 1997).
Logo:
(1995 e 1996)
e
(1996 e 1997)
A média dos dois é:
Passo 4
Assim, para 1997, temos os pares (1996 e 1997) e (1997 e 1998).
Logo:
(1996 e 1997) é igual ao de 1996
e
(1997 e 1998)
A média dos dois é:
Passo 5
Assim, para 1998, temos os pares (1997 e 1998) e (1998 e 1999).
Logo:
(1997 e 1998) é igual ao de 1997
e
(1998 e 1999)
A média dos dois é:
Passo 6
Assim, para 1999, temos os pares (1998 e 1999) e (1999 e 2000).
Logo:
(1998 e 1999) é igual ao de 1998
e
(1999 e 2000)
A média dos dois é:
Passo 7
Assim, para 2000, temos os pares (1999 e 2000) e (2000 e 2001).
Logo:
(1999 e 2000) é igual ao de 1999
e
(2000 e 2001)
A média dos dois é:
Passo 8
Assim, para 2001, temos os pares (2000 e 2001) e (2001 e 2002).
Logo:
(2000 e 2001) é igual ao de 2000
e
(2001 e 2002)
A média dos dois é:
Passo 9
Assim, para 2002, temos os pares (2001 e 2002) e (2002 e 2003).
Logo:
(2001 e 2002) é igual ao de 2001
e
(2002 e 2003)
A média dos dois é:
Passo 10
Assim, para 2003, temos os pares (2002 e 2003) e (2003 e 2004).
Logo:
(2002 e 2003) é igual ao de 2002
e
(2003 e 2004)
A média dos dois é:
Passo 11
E finalmente, para 2004, temos o par (2003 e 2004) é igual ao de 2003.
E podemos montar nossa tabela com todos os resultados obtidos.
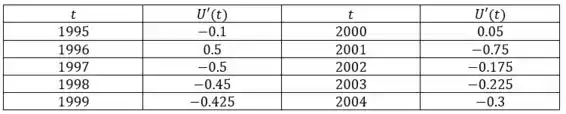
Resposta
