Se você tiver um SCA que possa calcular aproximações usando pontos médios e esboçar os retângulos correspondentes (use os comandos RiemannSum ou middlesum e middlebox no Maple), verifique a resposta do Exercício 11 e ilustre com um gráfico. Repita então com e .
Passo 1
Olá, meu amigo. Yuri aqui e estarei te guiando nesta atividade.
Aqui somos convidados a resolver a atividade, que nada mais é do que refazer a atividade 11 porém com um software de calculo matemático.
Eu não tenho o Maple, mas aqui está como você pode fazer isso usando o GeoGebra, que é gratuito.
Digite na caixa "Entrada":
Isso é automaticamente nomeado como "f(x)".
Aproxime (use a roda de scroll do mouse, ou clique no canto inferior esquerdo para usar o botão "Mover Vista Gráfica") e ajuste a janela para que você possa ver claramente o gráfico de x=0 até 1.
Clique no menu: Opções -> Arredondamento, para escolher 4 casas decimais.
Passo 2
Agora digite:
RectangleSum[f, 0, 1, 5, 0.5]
para fazer a Regra do Ponto Médio usando a função de até , usando retângulos. O "" significa usar o valor de onde está na metade do caminho desde o início de um subintervalo.
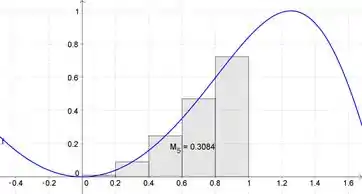
Agora, para retângulos, insira:
RectangleSum[f, 0, 1, 10, 0.5]
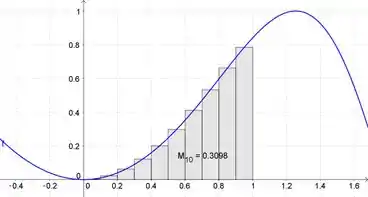
Passo 3
Agora, para retângulos, insira:
RectangleSum[f, 0, 1, 20, 0.5]
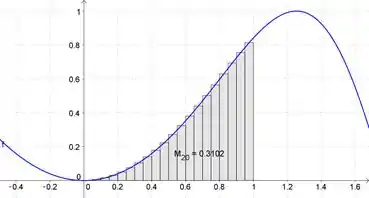
Resposta
Ver o desenvolvimento