Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Introdução aos polinômios

Ver Todos os Exercícios

Teoria

Fala galera! Vamos falar um pouco de alguém que você vai querer como amigo, porque você vai ver toda hora a partir de agora: os polinômios.

Os polinômios estão com tudo e merecendo até um capítulo só para eles. Mas, não é à toa. Os caras estão em todas! Então é melhor ficar bem ligado.

Então vamos lá:

Os polinômios são expressões como:

x 5 + 2 x - 1

x 2 - 2 x

x - 1

Sabe o que tem em comum nesses termos? Vários x elevados a algum número sendo somados!

Ou seja, um polinômio é qualquer expressão na forma: a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 + … + a 1 x + a 0

Onde os a ’s são constantes reais, podendo valer zero. Tipo assim, a 1 = 1 , a 2 = 0 e a 3 = 4 ...

E as potências de x são números sempre naturais.

Ou seja, não são polinômios:

x 3 + 2 x

x 5 / 2 + 1

x 3 - 5 x - 2 + 3 x

Pois tem expoentes não-naturais.

Ordem do polinômio

Até aqui, tudo bem? Então, vamos continuar. A ordem do polinômio é igual ao expoente da potência mais alta com coeficiente não nulo do polinômio, ou seja:

x 2 + 2 x + 1

É um polinômio de grau ou ordem 2 (ou de segundo grau), já que a potência mais alta é a do x 2 .

Outro exemplo:

0 ⋅ x 4 + 2 x 3 + 1

Aqui, apesar do x 4 ser a maior potência, ele tá multiplicado por zero e isso não vale! Então temos um polinômio de grau 3!

Nomenclatura

O termo “poli” de polinômio indica várias. Várias o que? Várias potências de base x .

Assim, quando temos somente uma potência presente, podemos chamar o polinômio de monômio, com “mono” de único, como em:

x 2

Há também, binômios, com dois:

x 3 + 1

E assim sucessivamente até o cara que fez a questão cansar de contar e falar que é polinômio mesmo.

Valor Numérico

Pessoal, agora se segurem nas cadeiras que vamos ver um tópico muito difícil! Mentira, você vai ver que é mel na chupeta! Imagina que temos o seguinte polinômio:

x 3 + 2 x 2 - 1

Muitas vezes, ele vai ser representado com P ( x ) , ou seja:

P x = x 3 + 2 x 2 - 1

Daí, o cara te pergunta: qual o valor do polinômio quando x = 1 ?

O que você precisa fazer? Simples, só colocar o 1 aonde tiver x e fazer as contas

1 3 + 2.1 2 - 1 = 2

Representamos assim

P 1 = 2

Igualdade de polinômios

Bom, agora vou te contar uma parada que é pra você não ser mais enganado de forma alguma! Se liga:

x 2 + 2 x + 1

x 2 + 3 x + 1

Se eu te disser que esses dois polinômios são iguais, você acredita? NÃO ACREDITE, É MENTIRA!

Dois polinômios só são iguais quando TODOS os seus coeficientes são iguais! Então:

x 2 + 2 x + 1

x 2 + 2 x

NÃO SÃO IGUAIS, pois o termo independente é diferente. Preste atenção nesse detalhe!

Aplicações

Meu anjo, eu sei que você deve estar pensando: “Mas por que raios isso aparece sempre?” “Por que eu estudo isso desde que eu me entendo por gente”

A resposta é a seguinte: OS POLINÔMIOS ESTÃO POR TODA PARTE!

Se eu te digo que tenho um quadrado de lado L e te pergunto a área dele, o que você me diz?

L 2

Isso é um polinômio!!! E se eu te pergunto o perímetro?

4 L

Também é um polinômio! Então não menospreze! Ele é muito é importante e provavelmente é a coisa que você mais usou na sua vida inteira!

Agora, partiu exercícios!

Ordem do polinômio

Nomenclatura

Valor Numérico

Igualdade de polinômios

Aplicações

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Classifique como polinômio ou não

a )   2 x 3 + x + 4

b )   x 3 + 3 x - 4

c ) 1 x 2 + 2 x

d )   x 1.3 + x - 7

Passo 1

(a)

Temos aí coeficientes constante e x com expoentes sempre naturais ( 3,1 , 0 ) . Logo, é um polinômio.

Passo 2

(b)

Temos uma raiz em cima do x 3 , levando a:

x 3 = x 3 1 2 = x 3 2

Como 3 / 2   não é natural, não se trata de um polinômio.

Passo 3

(c)

Temos um termo 1 / x 2 que é a mesma coisa que:

x - 2

Como - 2 não é natural, não é um polinômio.

Passo 4

(d)

Novamente temos aí 1.3 que não é natural, logo também não será um polinômio.

Resposta

a) Polinômio

b) Não-polinômio

c) Não-polinômio

d) Não-polinômio

Exercício Resolvido #2

Elaboração Própria

Dados os polinômios P x = x 4 - 3 x 2 + 7 x e Q x = 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1 , determine:

a   P x + Q ( x )

b   P x . Q ( x )

c   Q x - P ( x )

Diga qual o grau de cada polinômio encontrado nas alternativas.

Passo 1

FAAAAALA AÍ, meu aluno mais dedicado ever!!! Bora começar essa questãozinha do começo:

a   P x + Q x

Ora, você lembra quem são esses caras?

P x = x 4 - 3 x 2 + 7 x

Q x = 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1

Show, agora para somar esses caras, basta somarmos os termos semelhantes:

P x + Q x = x 4 - 3 x 2 + 7 x + 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1

P x + Q x = 9 x 5 + 1 - 3 x 4 + 2 x 3 + - 3 + 1 x 2 + 7 x - 1

P x + Q x = 9 x 5 - 2 x 4 + 2 x 3 - 2 x 2 + 7 x - 1

Bom, o grau desse polinômio que encontramos é a potência de maior valor, que no nosso caso é 5 . Logo, o grau do polinômio é 5 .

Passo 2

Bora pra próxima!

b   P x . Q x

Agora precisamos fazer a multiplicação entre os polinômios:

P x . Q x = x 4 - 3 x 2 + 7 x . 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1

É só fazer o chuveirinho:

P x . Q x = x 4 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1 - 3 x 2 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1 + 7 x 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1

P x . Q x = 9 x 9 - 3 x 8 + 2 x 7 + x 6 - x 4 - 27 x 7 + 9 x 6 - 6 x 5 - 3 x 4 + 3 x 2 + 63 x 6 - 21 x 5 + 14 x 4 + 7 x 3 - 7 x

Finalmente, juntando os termos:

P x . Q x = 9 x 9 - 3 x 8 - 2 5 x 7 + 73 x 6 - 27 x 5 + 10 x 4 + 7 x 3 + 3 x 2 - 7 x

Prontinho. E o grau desse polinômio é 9 .

Lembrando que para o grau de um produto de polinômios, basta somar o grau de cada um.

No nosso caso: grau de P x é 4 e o grau de Q ( x ) é 5 . Logo, o grau de P x . Q x = 4 + 5 = 9 .

Passo 3

Dá uma olhada nessa última:

c   Q x - P ( x )

Agora nós vamos subtrair um polinômio do outro:

Q x - P x = 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1 - x 4 - 3 x 2 + 7 x

Não se esqueça, só operamos os termos semelhantes (que têm o mesmo grau):

Q x - P x = 9 x 5 - 3 x 4 + 2 x 3 + x 2 - 1 - x 4 + 3 x 2 - 7 x

Q x - P x = 9 x 5 - 4 x 4 + 2 x 3 + 4 x 2 - 7 x - 1

E o grau desse amigo é 5 , que é o maior expoente.

Resposta

a   P x + Q x = 9 x 5 - 2 x 4 + 2 x 3 - 2 x 2 + 7 x - 1   e   o   p o l i n ô m i o   t e m   g r a u   5

b   P x . Q x = 9 x 9 - 3 x 8 - 25 x 7 + 73 x 6 - 27 x 5 + 10 x 4 + 7 x 3 + 3 x 2 - 7 x   e   o   p o l i n ô m i o   t e m   g r a u   9

c   Q x - P x = 9 x 5 - 4 x 4 + 2 x 3 + 4 x 2 - 7 x - 1   e   o   p o l i n ô m i o   t e m   g r a u   5

Exercício Resolvido #3

Elaboração Própria

Seja

P x = 2 x 3 + 3 x 2 + x + 4

Então dê o valor de P 1 ,   P ( - 2 ) e P ( 0 ) .

Passo 1

Se P x = 2 x 3 + 3 x 2 + x + 4 , para achar P ( 1 ) , basta substituir x por 1 :

P 1 = 2 1 3 + 3 1 2 + 1 + 4 = 10

Passo 2

Da mesma maneira:

P - 2 = 2 - 2 3 + 3 - 2 2 - 2 + 4 = 2 ⋅ - 8 + 3 ⋅ 4 - 2 + 4 = - 2

Passo 3

E também:

P 0 = 2 0 3 + 3 0 2 + 0 + 4 = 4

Resposta

P 1 = 10

P - 2 = - 2

P 0 = 4

Exercício Resolvido #4

Elaboração Própria

Determine o grau de cada um dos polinômios abaixo:

  1. h x = x 2 + 3 x - 1  
  2. p x = 3 x - 2
  3. g x = 5

Passo 1

Oláááá!!! Queremos identificar qual o grau de cada um dos polinômios, certo? E como podemos identificar o grau de um polinômio?

Basicamente o grau de um polinômio é o expoente máximo que ele possui. Não ficou claro?! Vamos ver então na pratica como vai funcionar? Vem comigo!!

Passo 2

a) O primeiro polinômio que precisamos determinar o grau é o

Para facilitar a nossa vida, vamos reescrever o polinômio da seguinte maneira:

Se você reparar, o termo sem o x é como se tivéssemos o x 0 acompanhando o termo, pois x 0 = 1 , beleza?!

Agora vamos lá! O maior expoente é o 2 , concorda?!

Então o polinômio tem grau 2, e por ter grau 2 também podemos chama-lô de binômio.

Show de bola?!

Passo 3

b) Vamos utilizar o mesmo raciocínio para o polinômio

Podemos reescrever da seguinte forma

Opa! Já da pra identificar que o maior expoente é o 1 !

Então o grau do nosso polinômio é 1!

Passo 4

c) Pra terminar, temos o polinômio

Beleza, mas não temos nenhum x aqui? Vai funcionar da mesma forma que os anteriores??

Vai sim, meu pupilo! Podemos reescrever da seguinte forma pra ficar mais claro:

Ou seja, o maior expoente aqui é o 0 ! Então o nosso polinômio tem grau 0 !

Beleza?!

Resposta

  1. Grau 2
  2. Grau 1
  3. Grau 0

Exercício Resolvido #5

Elaboração Própria

Determine o valor do polinômio

p x = 4 x 3 - 2 x 2 + 3 x + 106

Para x = 3 .

  1. 200
  2. 204
  3. 205
  4. 206
  5. 208

Passo 1

Fala Aíí!! Tudo certinho?! Nesse exercício queremos calcular o valor do polinômio quando x = 3 . Certo?

Então vamos substituir tudo o que for x por 3 !!

Passo 2

Vamos lá!! Temos o polinômio

E queremos calcular o valor numérico do polinômio para quando x = 3 . Ou seja, estamos querendo calcular p 3 !!

Então, substituindo x = 3 , temos

Beleeeeza... Agora é só partir para as continhas!!

Fazendo as multiplicações, ficamos com

Pra finalizar,

Beleza?!

Resposta

Letra C

Exercício Resolvido #6

Elaboração Própria

Considerando os polinômios

p x = 2 x 2 - 3

q x = 3 x 3 + 3 x 2 - 2 x

h x = x 3 - 1

Calcule q x + 2 h x - p ( x ) .

Passo 1

OPAA!!! Vamos lá!! Nosso objetivo aqui é calcular

q x + 2 h x - p ( x )

Então vamos começar pelo começo!

Vamos substituir os polinômios que foram dados no enunciado e fazer as continhas!!

Passo 2

Estamos considerando os polinômios

Então vamos substituir na expressão

Assim, ficamos com

Beleeeeza?!

Passo 3

Agora precisamos fazer as continhas!! Primeiro vamos fazer a multiplicação do 2 ( x 3 - 1 ) . Para isso, vamos usar o famoso chuveirinho:

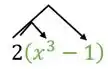
Assim, ficamos com

Beleza, temos então

Que é a mesma coisa que

Agora precisamos somar os termos que tem x 3 , x 2 , x e termo independente:

E assim ficamos com

Show de bola?!

Resposta

5 x 3 + x 2 - 2 x + 1

Exercício Resolvido #7

Elaboração Própria

Faça a multiplicação dos polinômios

p x = x 4 - 3 x 2

q x = 2 x 2 + 2 x 3 - 4

Passo 1

Vamos lá!!! Queremos realizar a mutiplicação dos polinômios

p ( x ) ∙ q x

Ou seja,

( x 4 - 3 x 2 ) ∙ ( 2 x 2 + 2 x 3 - 4 )  

Como faremos isso? Faremos a multiplicação distributiva!

Passo 2

Faremos a multiplicação de termo a termo entre os dois polinômios. Será o famoso “chuveirinho” ahahaha. Primeiro vamos multiplicar o x 4 por todos os termos do polinômio q ( x ) :

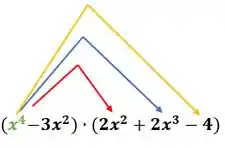
Ficando com

Beleza?!

Agora vamos fazer a mesma coisa pro segundo termo - 3 x 2 do polnômio p x : Vamos multiplicar ele por todos os termos do polinômio q ( x ) :

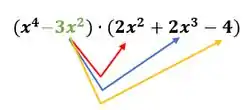
Fazendo as multiplicações, ficamos com

Agora juntando os dois, temos

Show de bola?!

Passo 3

Podemos simplificar os termos com o mesmo expoente:

E assim, temos

Beleza?!

Resposta

12 x 2 - 10 x 4 - 6 x 5 + 2 x 6 + 2 x 7

Exercício Resolvido #8

Elaboração Própria

Determine m para que P x = m - 3 x 3 + m 2 - 9 x 2 + m + 3 x + 3 seja um polinômio do segundo grau.

Passo 1

FAAAALA AÍ!!! Bora resolver essa questão. Bom, para termos um polinômio do segundo grau, precisamos que a maior potência seja 2 .

Então, o coeficiente que acompanha o x 3 tem que ser IGUAL a 0 e o que acompanha x 2 tem quer DIFERENTE de 0 .

Ora, quem acompanha o x 3 é ( m - 3 ) , então:

m - 3 = 0

Temos que:

m = 3

E quem acompanha o x 2 é m 2 - 9 , então:

m 2 - 9 ≠ 0

m ≠ 3   e   m ≠ - 3

Passo 2

Ora, eu estou confusa. Para ser um polinômio do segundo grau, descobrimos que m = 3 e m ≠ 3 ao mesmo tempo, então NÃO EXISTE m que satisfaça essa condição, portanto, não temos como ter um polinômio do segundo grau nesse caso,

Resposta

Não existe m que faça com que o polinômio seja do segundo grau.

Exercício Resolvido #9

Elaboração Própria

Determine A e B para que os polinômios P x = A + 2 B x 2 + ( 2 B - A ) x + 1 e Q x = 3 x 2 + x + 1 sejam iguais.

Passo 1

OI, MEU AMOOOOR!!! (Tomara que seu crush não seja ciumento)

Para ter uma igualdade entre polinômios, é necessário que TODOS os seus coeficientes sejam iguais.

Então, se queremos que esses polinômios P ( x ) e Q ( x ) sejam iguais, vamos tentar encontrar valores para A e B que satisfaçam essa condição.

A + 2 B = 3 2 B - A = 1 1 = 1

Concorda comigo? Eu igualei todos os coeficientes dos termos de cada polinômio.

Perceba que se os termos independentes fossem diferentes, já nem adiantaria tentar encontrar A e B , pois esses polinômios já seriam diferentes. Por este motivo eu coloquei ali um 1 = 1 , para você ver que podemos prosseguir com nosso cálculo.

Passo 2

Agora é resolver o sistema! Somando as duas primeiras equações, temos:

4 B = 4

B = 1

E portanto:

A + 2.1 = 3

A = 1

Logo, para que P ( x ) e Q ( x ) sejam iguais, precisamos que: A = B = 1 .

Resposta

A = 1

B = 1

Exercício Resolvido #10

Elaboração Própria

O perímetro de um triângulo retângulo é 6 e a hipotenusa é x . Exprima a área do triângulo como função de x .

Passo 1

Olááá, meu anjo! Como eu te disse na teoria, é muito comum, em polinômios, aparecer questões de modelagem de área ou volume, etc.

Primeiramente, vamos desenhar o que temos até agora:

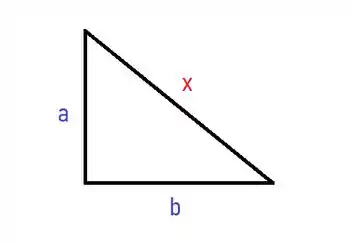
Esse é o desenho! Agora vamos escrever matematicamente o que ele diz em “o perímetro é 6 ”:

a + b + x = 6

E quando ele diz que é um triângulo retângulo, podemos assumir:

x 2 = a 2 + b 2

Passo 2

Maneiro, e o que queremos é:

Á r e a   d o   t r i â n g u l o = 1 2 b a s e × a l t u r a

S = a . b 2

Vamos ter que manipular as duas equações que temos para obter esse produto a . b em função de x .

Passo 3

Comecemos com a seguinte equação:

a + b + x = 6

Bom, a gente sabe que na outra equação temos um a 2 + b 2 , e a única forma desses termos aparecerem é se fizermos as seguintes manipulações:

a + b = 6 - x

a + b 2 = 6 - x 2

a 2 + 2 a . b + b 2 = 6 - x 2

E olha só o que apareceu!!!

a 2 + b 2 + 2 a . b = 6 - x 2

Eu não expandi o lado direito da igualdade por não haver nada que vá nos ajudar!

Passo 4

Agora, da outra equação temos:

a 2 + b 2 = x 2

Então podemos substituir essa relação nesta equação:

a 2 + b 2 + 2 a . b = 6 - x 2

Substituindo:

x 2 + 2 a . b = 6 - x 2

OPAAAAAA, encontramos a . b em função de x !!! Ainda não viu? Saca só:

2 a . b = 6 - x 2 - x 2

Ao simplificarmos os termos, ficamos com:

2 a . b = x 2 - 12 x + 36 - x 2

2 a . b = 36 - 12 x

Dividindo todo mundo por 2, ficamos assim:

a . b = 18 - 6 x

Passo 5

Finalmente, substituindo onde queríamos desde o início:

S = a . b 2

S = 18 - 6 x 2

S = 9 - 3 x

Resposta

S = 9 - 3 x

Exercícios de Livros Relacionados

Classifique cada função como potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial, ou função logarítmica. d) u t
Classifique cada função como potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial, ou função logarítmica.b) y =
Classifique cada função como potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial, ou função logarítmica. d) u t
Classifique cada função como potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial, ou função logarítmica. c) y =