Retrato de Fase e Classificação de Ponto Crítico – Caso Não Linear
Produzido por Carolina SabaTeoria
Quando tivermos um sistema não linear, para analisar cada ponto devemos, primeiro, fazer a matriz jacobiana. Jacobiana?! WTF?! Calma, considerando e a jacobiana nada mais é do que:
Depois substituímos os valores do ponto crítico na matriz, e vai ser essa matriz que vamos analisar. Sacou?
Vamos ver um exemplo.
Isolando na equação de baixo vamos ter
Substituindo isso na equação de cima, vamos ter
Isso nos diz que , e os pontos críticos vão ser
Pronto já encontramos os pontos críticos.
Aqui temos
A matriz jacobiana vai ser
Teríamos que analisar e que são os pontos críticos, entendeu? Depois é só consultar as relações que nós já vimos na teoria de retrato de fase para um caso linear. Vamos colocar a classificação aqui pra vocês lembrarem.
Classificação dos Pontos Críticos
Autovalores Reais Diferentes – Sinais Iguais e valores diferentes de
Vamos começar vendo o caso mais básico. A figura base vai ser
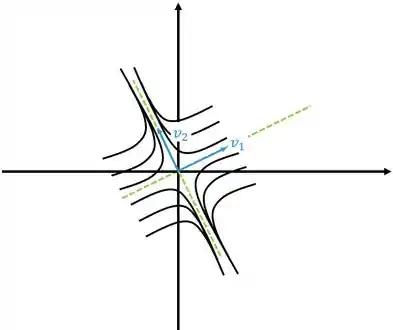
Repara que eu desenhei duas retas verdes ali, elas são as direções dos autovetores, é importante saber essas direções só para se ter uma ideia se o gráfico está mais ou menos inclinado, quando ele pede para esboçar não vamos nos preocupar muito com isso.
Se tivermos o sinal dos autovalores positivos o gráfico vai se afastar da origem, ficando
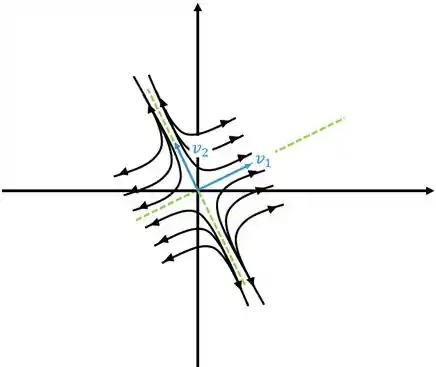
Neste caso o ponto crítico é chamado de nó instável ou repulsor.
Se tivermos o sinal dos autovalores negativos o gráfico vai se aproximar da origem, ficando
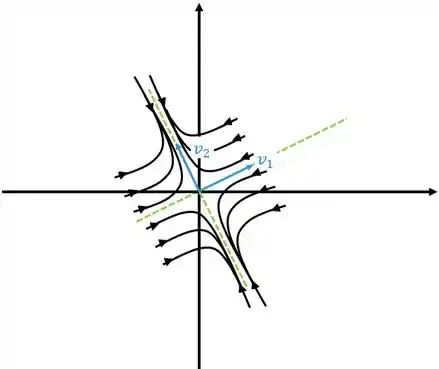
Neste caso o ponto crítico é chamado de nó estável ou atrator.
Entendeu agora a ideia de positivo se afastas da origem e negativo se aproximar?
Vamos ver o próximo caso
Autovalores Reais Diferentes – Um deles sendo
A grande diferença é que aqui vamos ter uma direção só e as setinhas vão sair perpendicular a essa direção.
Vamos chamar de o autovetor de e o outro autovetor. Assim o gráfico vai ser
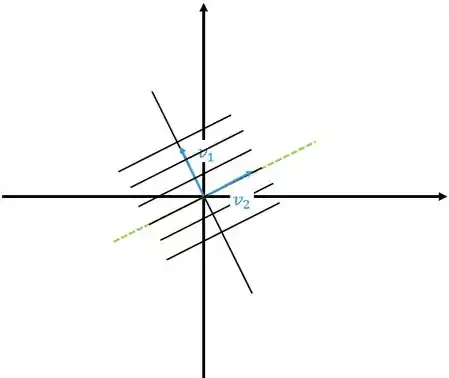
Se afastando se o outro autovalor for positivo, como o gráfico abaixo
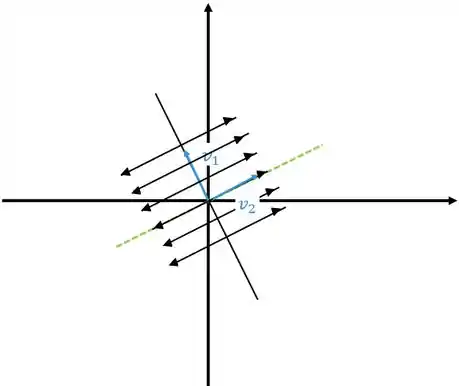
Neste caso o ponto crítico é chamado de nó instável ou repulsor.
e se aproximando se o outro autovalor for negativo, como o gráfico abaixo
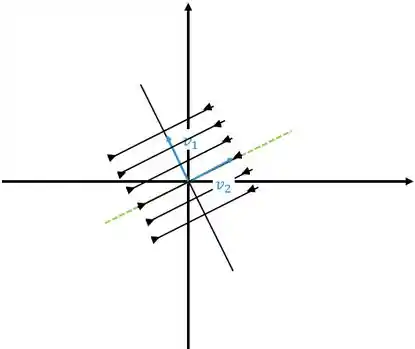
Neste caso o ponto crítico é chamado de nó estável ou atrator.
Os próximos exemplos vou colar direto qual o positivo e qual o negativo, mas tenta fixar na mente aquele truque, grava como é a figura, vai se aproximando se tivermos algo negativo e vai se afastando se tivermos algo positivo, o que vai variar o sinal de cada caso
Autovalores Reais Diferentes – Com sinais diferentes
Aqui a figura vai ficar
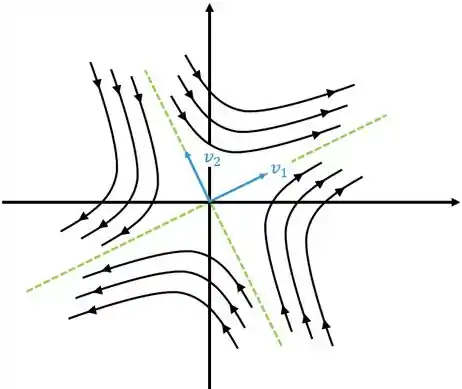
Neste caso o ponto crítico é chamado de ponto de sela.
Diferentes dos casos anteriores esse vai ter um formato só, que é esse aqui de cima.
Autovalores Reais Iguais – Autovetores
Aqui é bem de boa, vamos ter retas saindo da origem, duas delas vão ter as direções dos autovetores. Quando tivermos os autovalores positivos o retrato de fase vai ficar
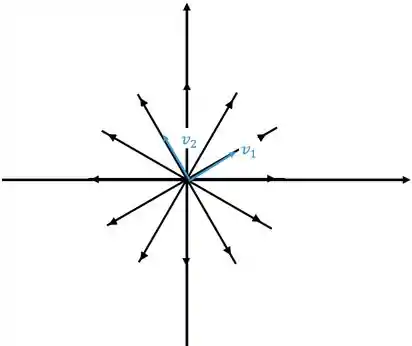
Neste caso o ponto crítico é chamado de nó Próprio ou estrela.
Quando os autovalores forem negativos vai ficar
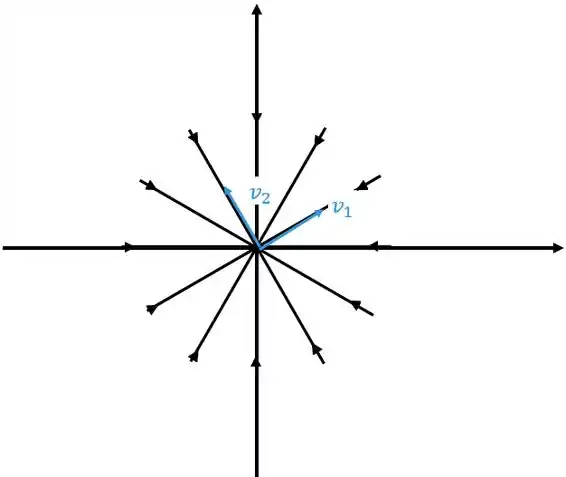
Neste caso o ponto crítico é chamado também de nó próprio ou estrela.
Autovalores Reais Iguais – 1 Autovetor
Aqui é o caso mais complicadinho, vamos precisar olhar com calma a orientação dos dois vetores.
Aqui temos o autovetor que vamos achar pelo método normal, ou seja, resolvendo , o outro vetor vamos achar fazendo
Fique atento em quem é e porque essa parada é algo rotacionado de uma forma que depende da orientação de cada um.
As retas paralelas vão ser definidas por , enquanto a direção da forma vai depender de .
Vamos ver uns desenhos para entender melhor, por enquanto vamos ignorar o fato do autovalor ter sinal ou não. Já sabemos que a figura fica igual o que muda na verdade é se vai se aproximar ou se afastar da origem.
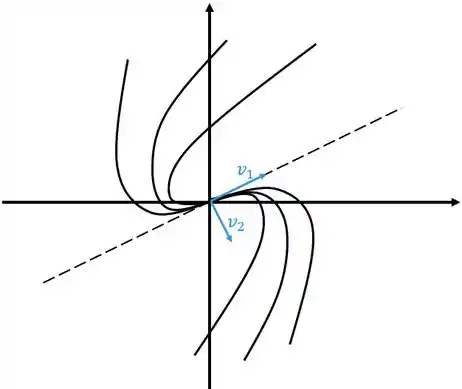
Reparou que o “desenho” sai para o lado onde os dois estão apontando? Vai ser sempre assim, olha outro desenho
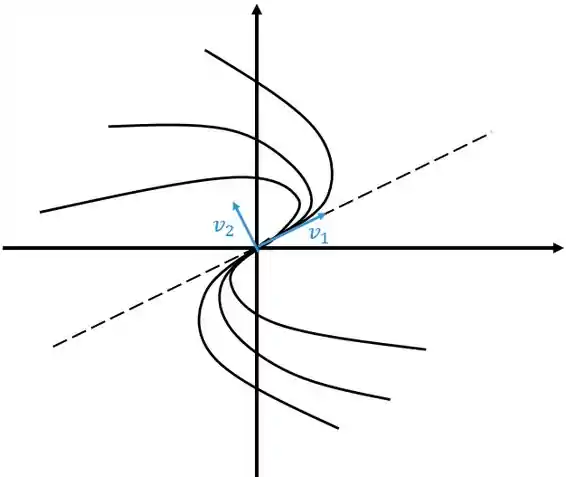
Sacou comé? Só falta completar a direção que as “setinhas” vão ficar, mas agora você já está careca de saber né? Vou repetir porque nunca é ruim relembrar rs, se for positivo vai se afastar da origem, se for negativo vai se aproximar da origem.
Neste caso o ponto crítico é chamado de nó impróprio.
Autovalores Complexos – Possuindo parte Real diferente de
Aqui vamos ter autovalores complexos, mas tem um detalhe a mais: eles precisam ser da forma com ,ou seja, aquele cara não pode ter só componente de . Aqui o desenho é molezinha, é uma espiral se aproximando da origem se for negativo, como a figura abaixo
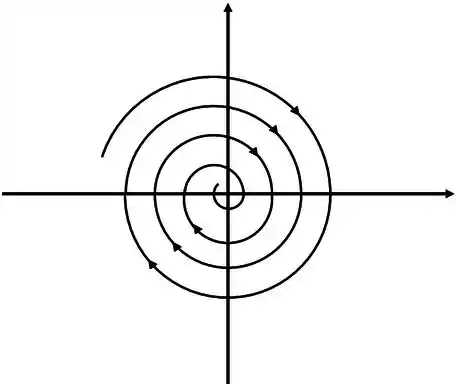
Neste caso o ponto crítico é chamado de espiral estável. Também pode ser chamado de espiral atrator.
E vai ser uma espiral se afastando da origem se for positivo
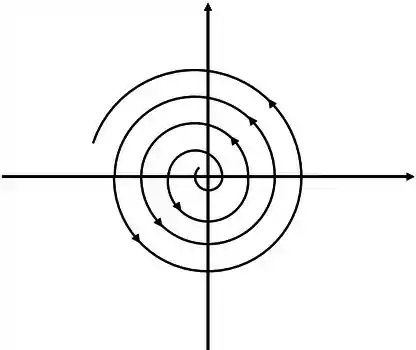
Neste caso o ponto crítico é chamado de espiral instável. Também pode ser chamado de espiral repulsor.
Autovalores Complexos – Possuindo parte Real igual a
Vamos ver como fica o último retrato de fase. Aqui é de boa também, vamos ter elipses com o mesmo centro, não se preocupe muito com a direção que ele roda, para saber direitinho isso precisaríamos das soluções do sistema.
Aqui vai uma figura para você ver como é
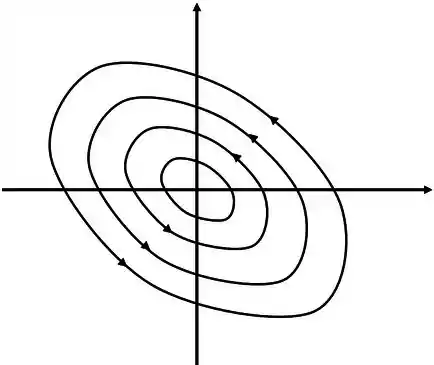
Neste caso o ponto crítico é chamado de centro.
Classificação dos Pontos Críticos
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine os pontos críticos e o retrato de fase, indicando qual tipo de ponto é o ponto crítico, no sistema abaixo.
Passo 1
Vamos começar achando os pontos críticos fazendo e
Vamos isolar na segunda equação
Substituindo na primeira equação vamos ter
E vamos ter
Os pontos críticos vão ser
Passo 2
Agora que temos os pontos vamos fazer a análise da matriz jacobiana, mas lembra como ela vai ficar?
Vamos ter
A matriz jacobiana vai ser
Passo 3
Vamos começar analisando o ponto , o jacobiano nesse ponto vai ficar
Vamos achar os autovalores desse cara
Resolvendo isso vamos ter
Vamos ter dois autovalores reais, ambos sendo positivos então esse ponto crítico é um nó instável.
Passo 4
Vamos agora para o ponto , o jacobiano nesse ponto vai ficar
Vamos achar os autovalores desse cara
Vamos ter
Vamos ter dois autovalores reais, com sinais trocados, então esse ponto crítico vai ser um ponto de sela.
Resposta
Os pontos críticos são , que é um nó instável, e que é um ponto de sela.
Exercício Resolvido #2
PUC-RJ, Cálculo 3, P2 2013.1, Questão 1
Considere o sistema abaixo que representa o comportamento de duas espécies( com densidades populacionais e ).
E
a) Determine as singularidades e classifique-as.
b) Esboce as trajetórias do sistema no primeiro quadrante.
c) Suponha que as populações iniciais em um laboratório sejam e . Interprete a evolução da população no tempo .
Passo 1
- Primeiramente, para determinar as singularidades fazemos
- Bom, vimos na questão anterior que que o ponto é um ponto de sela e o ponto é um ponto de centro.
- Agora usamos as condições inicias e e queremos interpretar a evolução das populações no tempo .
Ou seja,
Resolvendo as equações achamos como solução:
Que são as singularidades do sistema.
Passo 2
Para classifica-las então vamos achar a matriz jacobiana que é dada por
Onde e .
Então a matriz jacobiana aplicada ao nosso problema fica
Passo 3
Agora vamos aplicar a matriz nas nossas singularidades, isto é:
E
Passo 4
Vamos analisar primeira a matriz referente ao ponto .
Como é uma matriz diagonal seus autovalores são exatamente o elementos da diagonal, ou seja:
Portanto, como são dois autovalores reais e diferentes temos que o ponto é um ponto de sela.
Passo 5
Agora vamos analise a outra matriz referente ao ponto
Os autovalores são dados por
Ou seja, temos dois autovalores complexos com parte real nula o que caracteriza um ponto de centro.
Passo 6
E as separatrizes do retrato de fase são as retas
Portanto, no primeiro quadrante em torno de temos uma sela e em torno de temos um centro.
Passo 7
Como as coordenadas das condições iniciais são positivas, significa que a trajetória associada é fechada.
Mas o que isso significa??
Significa que a trajetória é periódica, isto é, se for essa trajetória então existe um tal que para todo real.
Isso implica que a evolução das duas espécies é periódica no tempo, sem que nenhuma delas desapareça.
Resposta
- é um ponto de sela e é um ponto de centro.
c) Isso implica que a evolução das duas espécies é periódica no tempo, sem que nenhuma delas desapareça.
Exercício Resolvido #3
PUC-RJ, Cálculo 3, P3 2013.2, Questão 1
Considere o problema abaixo que representa o comportamento de duas espécies (com densidades populacionais e ) competindo por suprimentos comuns.
- Determine as singularidades e classifique-as.
- Esboçe as trajetórias do retrato de fase no primeiro quadrante.
- Para quais condições iniciais existe uma configuração de equilíbrio na qual nenhuma espécie desaparece, e qual é esta configuração?
Passo 1
Resolvendo a letra a)
Pra encontrar as singularidades, devemos igualar as derivadas e a zero! E encontrar valores de e que satisfaçam o sistema. Vamos lá:
Com :
Com
Então, as singularidades são: . E agora devemos classificá-las!!
Passo 2
Pra classificá-las, devemos construir a matriz Jacobiana, que carrega as derivadas das expressões das populações em relação a e . Veja só:
E pra esse caso, a matriz será:
E utilizamos o critério de traço e determinante da matriz em cada singularidade pra classifica-las!
Pra
Portanto:
Então, é repulsor!
Pra :
Portanto:
Então, é sela!
Pra :
Portanto:
Então, é sela!
Pra :
Portanto:
Então, é atrator!
Passo 3
Resolvendo a letra b)
O retrato de fase será mais ou menos assim:
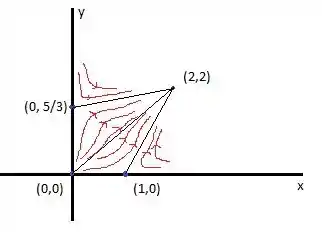
Passo 4
Resolvendo a letra c)
Como é atrator, qualquer condição inicial fora dos eixos irá convergir pra solução de equilíbrio . A única solução que não há extinção é a solução com dados iniciais ! Condições iniciais sobre os eixos resultam na extinção de pelo menos uma das duas espécies.
Resposta
a)