Retrato de Fase e Classificação de Ponto Crítico
Teoria
Introdução
Antes de saber fazer o retrato de fase é importante entendermos que diabos é isso, e para que ele serve, né?
Bem retrato de fase é a representação geométrica das trajetórias de um sistema de EDO. Boiou legal? Imagina o sistema aqui de baixo
Imagina que queremos representar a trajetória do vetor . Para isso vamos usar o retrato de fase. Ele vai servir como uma forma gráfica da resposta dessa paradinha.
Já vimos como ter as respostas de um sistema de EDO, agora vamos associar essas respostas com seus retratos de fase, ou seja, a representação geométrica da relação entre e .
Não fique chateado, é mais fácil do que parece.
Retratos de Fase – Sistema Linear
Para acharmos o retrato de fase de um sistema vamos precisar dos autovalores e autovetores.
Vamos sempre mostrar figuras de como é o gráfico básico do retrato de fase, na maioria dos casos vamos ter diferenciação de sinal dos caras. Quando isso acontecer basta usar um truque maroto e simples:
Se esse sinal for negativo, as trajetórias se aproximam da origem, enquanto que, se o sinal for positivo, as trajetórias se afastam da origem.
Em cada caso vamos ter uma figura e o nome da singularidade que ela vai ter.
O primeiro caso são os autovalores reais, só que aqui vamos quebrar isso em alguns subgrupos
Autovalores Reais Diferentes – Sinais Iguais e valores diferentes de
Vamos começar vendo o caso mais básico. A figura base vai ser
Repara que eu desenhei duas retas verdes ali, elas são as direções dos autovetores, é importante saber essas direções só para se ter uma ideia se o gráfico está mais ou menos inclinado, quando ele pede para esboçar não vamos nos preocupar muito com isso.
Se tivermos o sinal dos autovalores positivos o gráfico vai se afastar da origem, ficando
Neste caso o ponto crítico é chamado de nó instável ou repulsor.
Se tivermos o sinal dos autovalores negativos o gráfico vai se aproximar da origem, ficando
Neste caso o ponto crítico é chamado de nó estável ou atrator.
Entendeu agora a ideia de positivo se afastas da origem e negativo se aproximar?
Vamos ver o próximo caso
Autovalores Reais Diferentes – Um deles sendo
A grande diferença é que aqui vamos ter uma direção só e as setinhas vão sair perpendicular a essa direção.
Vamos chamar de o autovetor de e o outro autovetor. Assim o gráfico vai ser
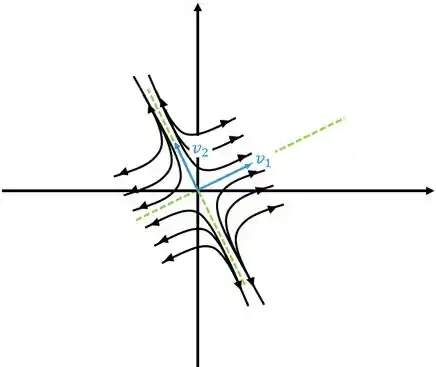
Se afastando se o outro autovalor for positivo, como o gráfico abaixo
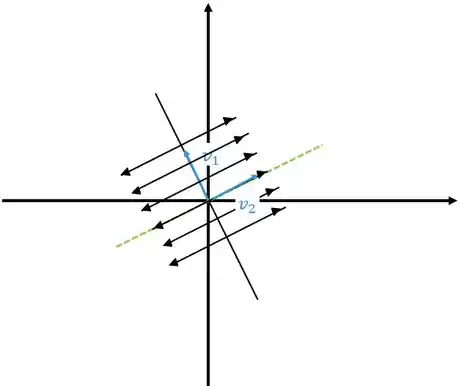
Neste caso o ponto crítico é chamado de nó instável ou repulsor.
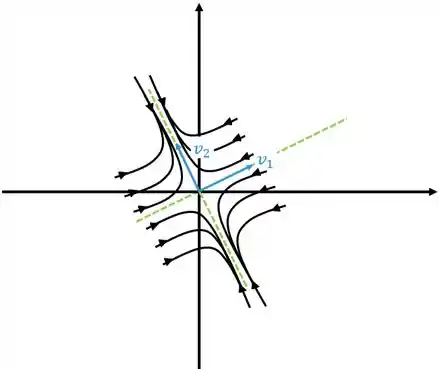
e se aproximando se o outro autovalor for negativo, como o gráfico abaixo
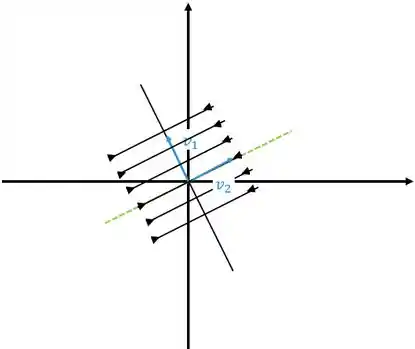
Neste caso o ponto crítico é chamado de nó estável ou atrator.
Os próximos exemplos vou colar direto qual o positivo e qual o negativo, mas tenta fixar na mente aquele truque, grava como é a figura, vai se aproximando se tivermos algo negativo e vai se afastando se tivermos algo positivo, o que vai variar o sinal de cada caso
Autovalores Reais Diferentes – Com sinais diferentes
Aqui a figura vai ficar
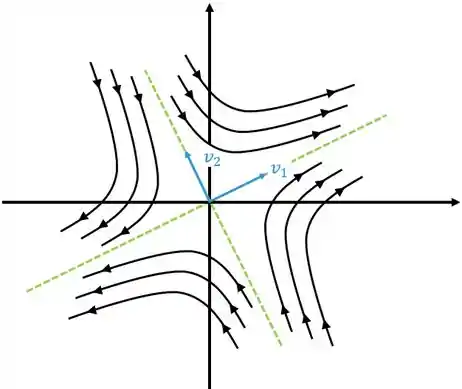
Neste caso o ponto crítico é chamado de ponto de sela.
Diferentes dos casos anteriores esse vai ter um formato só, que é esse aqui de cima.
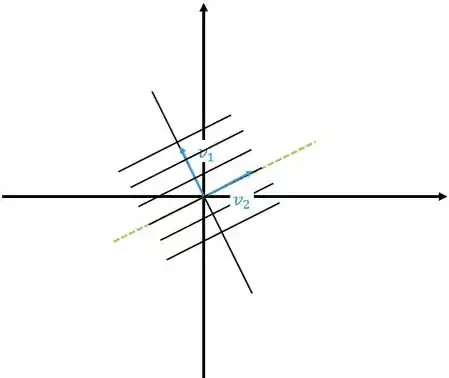
Autovalores Reais Iguais – Autovetores
Aqui é bem de boa, vamos ter retas saindo da origem, duas delas vão ter as direções dos autovetores. Quando tivermos os autovalores positivos o retrato de fase vai ficar
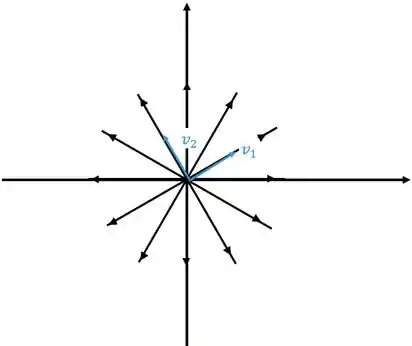
Neste caso o ponto crítico é chamado de nó Próprio ou estrela.
Quando os autovalores forem negativos vai ficar
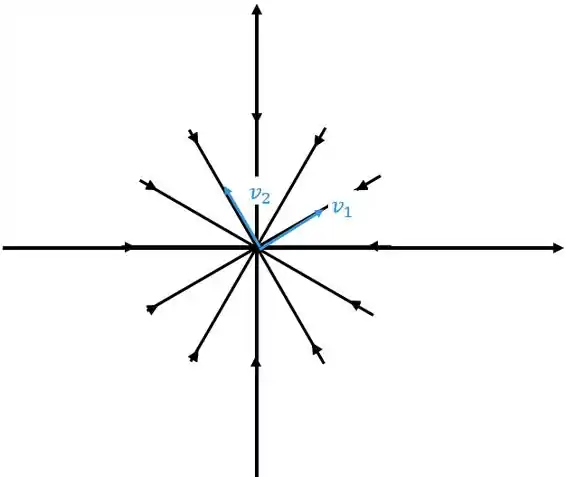
Neste caso o ponto crítico é chamado também de nó próprio ou estrela.
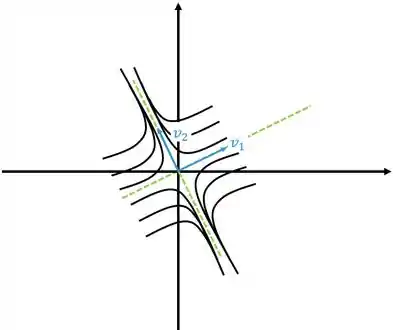
Autovalores Reais Iguais – 1 Autovetor
Aqui é o caso mais complicadinho, vamos precisar olhar com calma a orientação dos dois vetores.
Aqui temos o autovetor que vamos achar pelo método normal, ou seja, resolvendo , o outro vetor vamos achar fazendo
Fique atento em quem é e porque essa parada é algo rotacionado de uma forma que depende da orientação de cada um.
As retas paralelas vão ser definidas por , enquanto a direção da forma vai depender de .
Vamos ver uns desenhos para entender melhor, por enquanto vamos ignorar o fato do autovalor ter sinal ou não. Já sabemos que a figura fica igual o que muda na verdade é se vai se aproximar ou se afastar da origem.
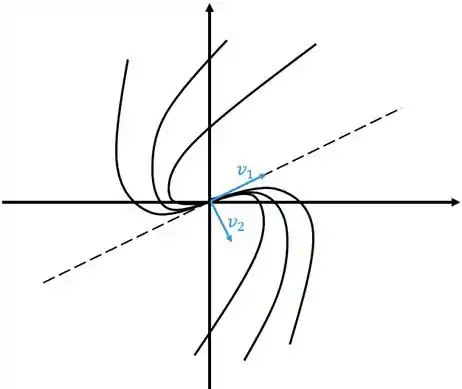
Reparou que o “desenho” sai para o lado onde os dois estão apontando? Vai ser sempre assim, olha outro desenho
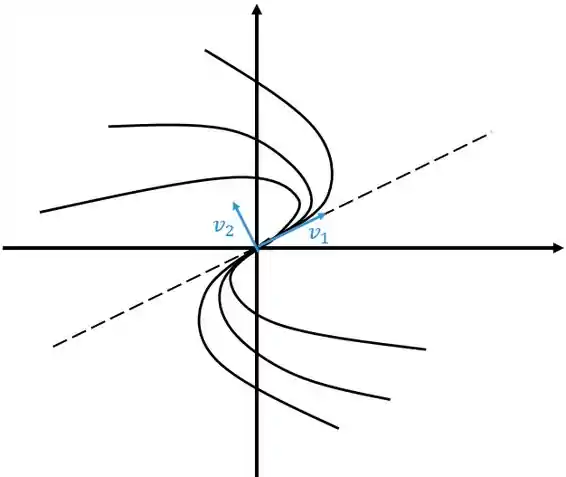
Sacou comé? Só falta completar a direção que as “setinhas” vão ficar, mas agora você já está careca de saber né? Vou repetir porque nunca é ruim relembrar rs, se for positivo vai se afastar da origem, se for negativo vai se aproximar da origem.
Neste caso o ponto crítico é chamado de nó impróprio.
Autovalores Complexos – Possuindo parte Real diferente de
Aqui vamos ter autovalores complexos, mas tem um detalhe a mais: eles precisam ser da forma com ,ou seja, aquele cara não pode ter só componente de . Aqui o desenho é molezinha, é uma espiral se aproximando da origem se for negativo, como a figura abaixo
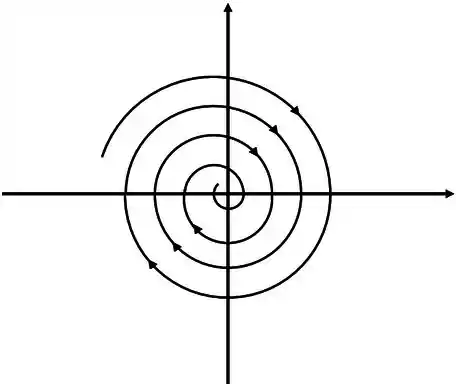
Neste caso o ponto crítico é chamado de espiral estável. Também pode ser chamado de espiral atrator.
E vai ser uma espiral se afastando da origem se for positivo
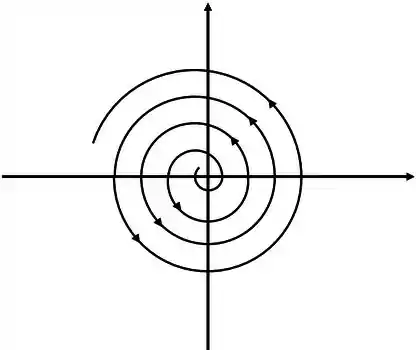
Neste caso o ponto crítico é chamado de espiral instável. Também pode ser chamado de espiral repulsor.
Autovalores Complexos – Possuindo parte Real igual a
Vamos ver como fica o último retrato de fase. Aqui é de boa também, vamos ter elipses com o mesmo centro, não se preocupe muito com a direção que ele roda, para saber direitinho isso precisaríamos das soluções do sistema.
Aqui vai uma figura para você ver como é
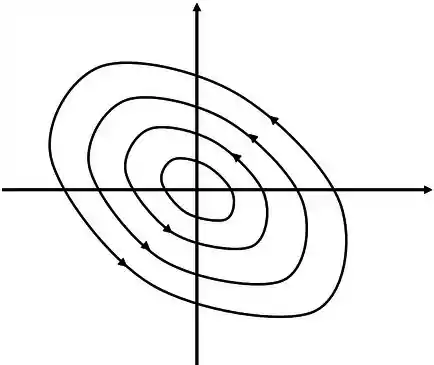
Neste caso o ponto crítico é chamado de centro.
Exercícios Resolvidos
Exercício Resolvido #1
PUC-RJ, Cálculo 3, P2 2012.2, Questão 4
Seja . Considere as matrizes seguintes:
A seguir estão os retratos de fase dos sistemas
Ao lado de cada figura escreva qual é a letra da matriz correspondente.
Passo 1
O macete desse questão é achar os autovalores das matrizes para que assim consigamos descobrir a cara do seu retrato de fase associado.
Vamos fazer cada matriz, uma de cada vez.
- Temos
Então
Então como um dos autovalores é zero e o outro é maior que zero, temos um ponto crítico repulsor, então o retrato de fase associado a esse sistema é o da figura (1).
Passo 2
Então,
Então, como os autovalores são complexos com parte real nula, temos um ponto crítico do tipo centro, portanto o retrato de fase associado a esse sistema é o da figura (3)
Passo 2
Então,
Então, como os autovalores são reais, diferentes e não nulos, temos que o retrato de fase da figura (6) representa o sistema c.
Passo 3
Então,
Como os autovalores são complexos com parte real maior que zero, temos uma espiral repulsora e portanto a figura (4) representa o retrato de fase associado ao sistema.
Passo 4
e)
Então,
Como os autovalores são complexos com a parte real menor que zero, temos uma espiral atratora portanto a figura (7) representa o retrato de fase associado ao sistema.
Passo 5
f)
Então,
Como os autovalores são negativos e diferentes entre si, temos um nó repulsor ou seja a figura (8) representa o retrato de fase do nosso sistema.
Passo 6
g)
Então, como é uma matriz diagonal, temos que os elementos da sua diagonal são seus autovalores, portanto
Como os autovalores são iguais e diferentes de zero, temos um nó repulsor e portanto a figura (5) representa o retrato de fase do sistema.
Passo 7
h)
Novamente, temos que os autovalores da matriz são os elementos da sua diagonal já é uma matriz triangular superior, portanto
E como temos autovalores reais e com sinais diferentes temos um ponto de sela e portanto a figura (2) representa o retrato de fase do sistema.
Resposta
Exercício Resolvido #2
Elaboração Própria
Sabendo que o ponto crítico do sistema abaixo é , determine o retrato de fase e qual tipo de ponto é o ponto crítico.
Passo 1
O sistema já está na forma matricial, então só precisamos fazer os autovalores de para achar seu retrato de fases.
A primeira coisa que devemos fazer é identificar o valor da matriz
Passo 2
Agora temos que achar o autovalores de .
Lembra é só fazer
Esse é o caso de autovalores iguais, aqui vai ser uma situação onde precisamos achar seus autovetores, porque se tivermos diretos é uma coisa se tivermos direto e depois ter que resolver aquela equação auxiliar vai ser diferente o retrato de fase.
Passo 3
Agora temos que achar os autoespaços associados, para isso vamos ter
Vamos ter
E o autovetor associado vai ser
Podemos tirar esse
Agora vimos que só rola um vetor, precisamos achar o outro autovetor usando
Vamos fazer
Então
Isso deixa a equação
O auto vetor vai ser
Essa parte com vamos ignorar porque já é o outro autovetor, então
Beleza agora conseguimos fazer um esboço melhor, aqui temos que achar o segundo porque precisamos saber como é a orientação dos dois para pode deixar direitinho o retrato de fases.
Passo 4
O retrato de fases vai ser
Neste caso o ponto crítico é chamado de nó impróprio.
Resposta
Neste caso o ponto crítico é chamado de nó impróprio.
Exercício Resolvido #3
PUC-RJ, Cálculo 3, P2 2013.1, Questão 3
Considere o sistema linear onde:
Determine os valores de a, b para os quais:
I) As soluções do sistema satisfazem
II) A singularidade (0,0) é uma sela hiperbólica.
Passo 1
A primeira coisa a se fazer em problemas desse tipo é achar os autovalores da matriz .
Então vamos lá!
Fazemos
Então achamos
Passo 2
Agora vamos analisar os valores e sinais de e
- e são não nulos e tem sinais opostos: Então os autovalores são complexos com a parte real diferente de zero e positiva.
- ou são iguais a zero: Daí o sistema possui somente um autovalor e (0,0) conitnua sendo repulsor.
- e não nulos e tem sinais iguais: Aí os autovalores são diferentes e um deles é sempre positivo, mais especificamente o autovalor .
Portanto o ponto é um ponto repulsor ou fonte então toda solução se afasta de quando aumenta.
Nesse caso temos: .
E nesse caso temos que o ponto é um ponto de sela hiperbólica.
Passo 3
Agora estamos prontos pra responder os itens I) e II).
I) Não existem valores de e que satisfaçam a condição
Pois como vimos antes, em todos os casos dos autovalores de A achamos que o ponto é um ponto repulsor, ou seja toda solução se afasta de quando aumenta.
Passo 4
II) Como vimos nos casos acima, o ponto é um ponto de sela hiperbólica quando e satisfazem
Resposta
- Não existem valores de e que satisfazem a condição.
- .